
| ����ʱ�� | ������ | �������� | |
| A�ͺ� | B�ͺ� | ||
| ��һ�� | 3̨ | 5̨ | 1800Ԫ |
| �ڶ��� | 4̨ | 10̨ | 3100Ԫ |
���� ��1����A��B�����ͺŵ���ȵ����۵��۷ֱ�ΪxԪ��yԪ������3̨A�ͺ�5̨B�ͺŵĵ�������1800Ԫ��4̨A�ͺ�10̨B�ͺŵĵ�������3100Ԫ���з�������⼴�ɣ�
��2����ɹ�A���ͺŵ����ą����ɹ�B���ͺŵ���ȣ�30-a��̨�����ݽ�����5400Ԫ���в���ʽ��⼴�ɵó��𰸣�
��3��������Ϊ1400Ԫ���з������a��ֵΪ20�������ϣ�2������������֪����ʵ��Ŀ�꣮
��� �⣺��1����A��B�����ͺŵĵ���ȵ����ۼ۷ֱ�Ϊx��yԪ��
��$\left\{\begin{array}{l}3x+5y=1800\\ 4x+10y=3100\end{array}\right.$��
��ã�$\left\{\begin{array}{l}x=250\\ y=210\end{array}\right.$��
��A��B�����ͺŵ���ȵ����۽�ֱ�Ϊ250Ԫ��210Ԫ��
��2����ɹ�A���ͺŵ����ą����ɹ�B���ͺŵĵ���ȣ�30-a��̨
��200a+170��30-a����540��
��ã�a��10��
�����ɹ�A���ͺŵĵ����10̨��
��3����������ã�
��2500-200��a+��210-170����30-a��=1400��
���a=20��
��a��10��
���ڣ�2�������³�����������30̨����Ȳ���ʵ������Ϊ1400Ԫ��Ŀ�꣮
���� ���⿼���˶�Ԫһ�η������һԪһ�β���ʽ��Ӧ�ã������Ĺؼ��Ƕ������⣬���δ֪�����ҳ����ʵĵ�����ϵ�Ͳ��ȹ�ϵ���з�����Ͳ���ʽ��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��ƽ���ı���ABCD�У�E��F�ǶԽ���BD�ϵ����㣬�ڲ������κθ����ߵ�����£��������һ������ʹ��ABE�ա�CDF�������ӵ�������BE=FD��BF=DE���1=��2���𰸲�Ψһ����
��ͼ��ƽ���ı���ABCD�У�E��F�ǶԽ���BD�ϵ����㣬�ڲ������κθ����ߵ�����£��������һ������ʹ��ABE�ա�CDF�������ӵ�������BE=FD��BF=DE���1=��2���𰸲�Ψһ�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\root{3}{-1}=-\root{3}{-1}$ | B�� | $\root{3}{-3}=\root{3}{3}$ | C�� | $\root{3}{-1}=\root{3}{{|{-1}|}}$ | D�� | $\root{3}{-1}=-\root{3}{1}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
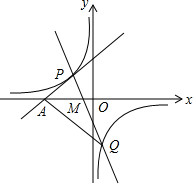 ��ͼ��ʾ��P��a��3����ֱ��y=x+5�ϵ�һ�㣬ֱ�� y=k1x+b��˫����y=$\frac{k}{x}$�ཻ��P��Q��1��m����
��ͼ��ʾ��P��a��3����ֱ��y=x+5�ϵ�һ�㣬ֱ�� y=k1x+b��˫����y=$\frac{k}{x}$�ཻ��P��Q��1��m�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
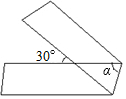 ��ͼ����һ�������εĿ�ֽ������ͼ�۵�����Ϧ�=��������
��ͼ����һ�������εĿ�ֽ������ͼ�۵�����Ϧ�=��������| A�� | 30�� | B�� | 60�� | C�� | 70�� | D�� | 75�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 3�� | B�� | 2�� | C�� | 1�� | D�� | 0�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
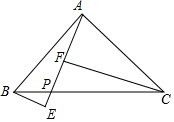 ��ͼ����֪�ڡ�ABC�У���BAC=90�㣬AB=AC����PΪBC����һ���㣨BP��CP�����ֱ��B��C��BE��AP�ڵ�E��CF��AP�ڵ�F����˵����EF=CF-BE��
��ͼ����֪�ڡ�ABC�У���BAC=90�㣬AB=AC����PΪBC����һ���㣨BP��CP�����ֱ��B��C��BE��AP�ڵ�E��CF��AP�ڵ�F����˵����EF=CF-BE���鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com