
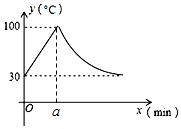 ���������ˮ����ͨ��Դ�ͽ����Զ�����������ʱÿ��������10�棬���ȵ�100�棬ֹͣ���ȣ�ˮ�¿�ʼ�½�����ʱˮ�£��棩�뿪������ʱ��min���ɷ�������ϵ��ֱ��ˮ�½���30�棬��ˮ���ػ�����ˮ���ػ����Զ��������ظ������Զ�������ˮ��Ϊ30��ʱ����ͨ��Դ��ˮ��y���棩��ʱ��x��min���Ĺ�ϵ��ͼ��
���������ˮ����ͨ��Դ�ͽ����Զ�����������ʱÿ��������10�棬���ȵ�100�棬ֹͣ���ȣ�ˮ�¿�ʼ�½�����ʱˮ�£��棩�뿪������ʱ��min���ɷ�������ϵ��ֱ��ˮ�½���30�棬��ˮ���ػ�����ˮ���ػ����Զ��������ظ������Զ�������ˮ��Ϊ30��ʱ����ͨ��Դ��ˮ��y���棩��ʱ��x��min���Ĺ�ϵ��ͼ������ ��1����������ͺ���ͼ��������a��ֵ��
��2�����ݺ���ͼ�������������y����x�ĺ�����ϵʽ��ע�⺯��ͼ����ѭ�����ֵģ�
��3�����ݣ�2���еĺ�������ʽ���Խ���⣻
��4����������ͣ�3���еĽ�����Խ���⣮
��� �⣺��1��������ɵã�
a=��100-30����10=70��10=7��
�ʴ�Ϊ��7��
��2����0��x��7ʱ����y����x�ĺ�����ϵʽΪ��y=kx+b��
$\left\{\begin{array}{l}{b=30}\\{7k+b=100}\end{array}\right.$����$\left\{\begin{array}{l}{k=10}\\{b=30}\end{array}\right.$��
����0��x��7ʱ��y����x�ĺ�����ϵʽΪy=10x+30��
��x��30ʱ����y=$\frac{a}{x}$��
100=$\frac{a}{7}$����a=700��
����x��30ʱ��y����x�ĺ�����ϵʽΪy=$\frac{700}{x}$��
��y=30ʱ��x=$\frac{70}{3}$��
��y��x�ĺ�����ϵʽΪ��y=$\left\{\begin{array}{l}{10x+30}&{��0��x��7��}\\{\frac{700}{x}}&{��7��x��\frac{70}{3}��}\end{array}\right.$��y��x�ĺ�����ϵʽÿ$\frac{70}{3}$�����ظ�����һ�Σ�
��3����y=70����y=10x+30����x=4��
��y=70����y=$\frac{700}{x}$����x=10��
��10-4=6��
����ˮ����6������ʹˮ�±�����70�漰���ϣ�
��4��������ɵã�
6+��70-20����10=11�����ӣ���
��40-11=29��
��8��29������ͨ��Դ�ȽϺ��ʣ�
���� ���⿼�鷴����������Ӧ�á�һ�κ�����Ӧ�ã������Ĺؼ�����ȷ���⣬�ҳ�����������Ҫ���������������ν�ϵ�˼��ͺ�����˼����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
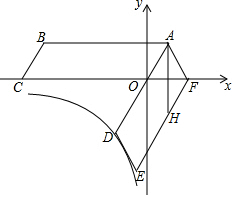 ��ͼ���ı���ABCO��ƽ���ı����ҵ�C��-4��0������ƽ���ı���ABCO�Ƶ�A��ʱ����ת�õ�ƽ���ı���ADEF��AD������O����Fǡ������x����������ϣ�����A��D�ڷ���������y=$\frac{k}{x}$��ͼ���ϣ���A��AH��x�ᣬ��EF�ڵ�H��
��ͼ���ı���ABCO��ƽ���ı����ҵ�C��-4��0������ƽ���ı���ABCO�Ƶ�A��ʱ����ת�õ�ƽ���ı���ADEF��AD������O����Fǡ������x����������ϣ�����A��D�ڷ���������y=$\frac{k}{x}$��ͼ���ϣ���A��AH��x�ᣬ��EF�ڵ�H���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
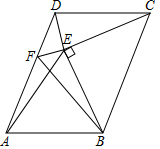 ��ͼ����?ABCD�У���BCΪб����?ABCD��������ֱ�ǡ�BCE������DE������E��EF��DE��AD�ڵ�F����CDE=��CED=��DCB��
��ͼ����?ABCD�У���BCΪб����?ABCD��������ֱ�ǡ�BCE������DE������E��EF��DE��AD�ڵ�F����CDE=��CED=��DCB���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | a+1 | B�� | a-1 | C�� | -a-1 | D�� | -a+1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
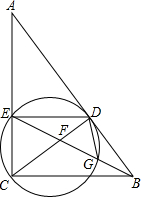 ��ͼ����Rt��ABC�У���ACB=90�㣬��D��AB��һ�㣬��CDΪֱ������O����AC�ڵ�E������BE�ֱ�CD�͡�O�ڵ�F��G������DE��DG���ҡ�BDG=��BED��
��ͼ����Rt��ABC�У���ACB=90�㣬��D��AB��һ�㣬��CDΪֱ������O����AC�ڵ�E������BE�ֱ�CD�͡�O�ڵ�F��G������DE��DG���ҡ�BDG=��BED���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 700��108 | B�� | 70��108 | C�� | 7��1010 | D�� | 0.7��109 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com