
 如图,在△ABC中,AD是∠BAC的平分线,E,F分别为AB,AC上的点,若DE=DF,且AE>AF,求证:∠EDF与∠BAF互补(提示:作DM⊥AB于点M,DN⊥AC于点N)
如图,在△ABC中,AD是∠BAC的平分线,E,F分别为AB,AC上的点,若DE=DF,且AE>AF,求证:∠EDF与∠BAF互补(提示:作DM⊥AB于点M,DN⊥AC于点N) 分析 过点D作DM⊥AB于点M,作DN⊥AC于点N,根据角平分线上的点到角的两边距离相等可得DM=DN,利用“HL”证明Rt△DEM和Rt△DFN全等,根据全等三角形对应角相等可得∠DEM=∠DFN,然后求出∠DEM+∠AFD=180°,再根据四边形的内角和等于360°求解即可.
解答  证明:如图,过点D作DM⊥AB于点M,作DN⊥AC于点N,
证明:如图,过点D作DM⊥AB于点M,作DN⊥AC于点N,
∵AD是∠BAC的平分线,
∴DM=DN,
在Rt△DEM和Rt△DFN中,$\left\{\begin{array}{l}{DE=DF}\\{DM=DN}\end{array}\right.$,
∴Rt△DEM≌Rt△DFN(HL),
∴∠DEM=∠DFN,
∵∠DFN+∠AFD=180°,
∴∠DEM+∠AFD=180°,
在四边形AEDF中,∠EDF+∠BAF=360°-(∠DEM+∠AFD)=360°-180°=180°,
∴∠EDF与∠BAF互补.
点评 本题考查了全等三角形的判定与性质,角平分线上的点到角的两边距离相等的性质,熟记性质并作辅助线构造出全等三角形是解题的关键.


 全能练考卷系列答案
全能练考卷系列答案科目:初中数学 来源: 题型:解答题
 已知抛物线y=-x2+bx+c与x轴交于点A和点B(3,0),与y轴交于点C(0,3),P是线段BC上一点,过点P作PN∥y轴交x轴于点N,交抛物线于点M.
已知抛物线y=-x2+bx+c与x轴交于点A和点B(3,0),与y轴交于点C(0,3),P是线段BC上一点,过点P作PN∥y轴交x轴于点N,交抛物线于点M.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 2017年 月 农历丙申(猴)年辛丑月 建国68年 | ||||||
| 日 | 一 | 二 | 三 | 四 | 五 | 六 |
| 1 初五 | 2 初六 | 3 立夏初七 | 4 初八 | |||
| a | d | |||||
| b | c | |||||
| A. | 3个 | B. | 2个 | C. | 1个 | D. | 0个 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
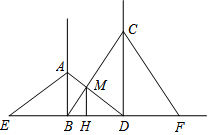 如图,工地上两根电灯杆相距a米,分别在高为4米、6米的A、C处用铁丝将两杆固定,则铁丝AD与铁丝BC的交点M处离地面米的高MH=$\frac{12}{5}$m.
如图,工地上两根电灯杆相距a米,分别在高为4米、6米的A、C处用铁丝将两杆固定,则铁丝AD与铁丝BC的交点M处离地面米的高MH=$\frac{12}{5}$m.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
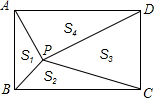 如图,点P是矩形ABCD内一点,连接PA、PB、PC、PD,已知AB=3,BC=4,设△PAB、△PBC、△PCD、△PDA的面积分别为S1、S2、S3、S4,以下判断:
如图,点P是矩形ABCD内一点,连接PA、PB、PC、PD,已知AB=3,BC=4,设△PAB、△PBC、△PCD、△PDA的面积分别为S1、S2、S3、S4,以下判断:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com