
����Ŀ��ij����ѧУ�����һ��ѧУ�Ƽ�һ��ѧ�������ݹ涨���Ƽ����������ɱ��꼶200��ѧ������ͶƱ��ÿ��ֻ���Ƽ�һ�ˣ�������ȨƱ����ѡ����Ʊ�����ļס��ҡ�������.ͶƱ���ͳ����ͼһ��

��Σ���������ѡ�˽����˱��Ժ������������.����ɼ����ұ���ʾ��ͼ����ijͬѧ�����ϱ����Ƶ�һ��������������ͼ.�������������Ϣ����������⣺
��1����ȫͼһ��ͼ��.
��2�������ÿ����ѡ�˵ĵ�Ʊ��.
��3����ÿ����ѡ�˵�һƱ��1�֣�ͶƱ�����ԡ���������÷ְ���2��5��3�ı�ȷ��������������ѡ�˵�ƽ���ɼ����ɼ��ߵĽ���¼ȡ��Ӧ��¼ȡ˭��
������Ŀ | ���Գɼ�/�� | ||
�� | �� | �� | |
���� | 92 | 90 | 95 |
���� | 85 | 95 | 80 |
���𰸡���1��ͼ����������2���ĵ�Ʊ��Ϊ68Ʊ���ҵĵ�Ʊ��Ϊ60Ʊ�����ĵ�Ʊ��Ϊ56Ʊ����3����ƽ���ɼ�Ϊ![]() �֣��ҵ�ƽ���ɼ�Ϊ
�֣��ҵ�ƽ���ɼ�Ϊ![]() �֣�����ƽ���ɼ�Ϊ
�֣�����ƽ���ɼ�Ϊ![]() �֣�¼ȡ��
�֣�¼ȡ��
��������
��1����1��ȥ�ס����������ĵ�Ʊ����ռ��Ʊ���İٷ��ʼ�������ҵĵ�Ʊ��ռ��Ʊ���İٷ��ʣ��ɱ����֪�������Գɼ�Ϊ85�֣�Ȼ��ȫͼһ��ͼ�����ɣ�
��2������Ʊ���˸���ѡ�˵ĵ�Ʊ����ռ�İٷ��ʼ��ɣ�
��3���������⣬������˵ļ�Ȩƽ���֣�Ȼ��Ƚϼ����жϣ�
�⣺��1���ҵĵ�Ʊ��ռ��Ʊ���İٷ���Ϊ��1��34%��28%��8%=30%
�ɱ����֪�������Գɼ�Ϊ85�֣�
��ȫͼһ��ͼ�����£�
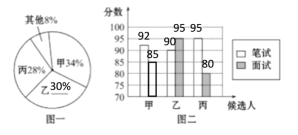
��2���ĵ�Ʊ��Ϊ��200��34%=68��Ʊ��
�ҵĵ�Ʊ��Ϊ��200��30%=60��Ʊ��
���ĵ�Ʊ��Ϊ��200��28%=56��Ʊ��
�𣺼ĵ�Ʊ��Ϊ68Ʊ���ҵĵ�Ʊ��Ϊ60Ʊ�����ĵ�Ʊ��Ϊ56Ʊ��
��3���������⣬��ƽ���ɼ�Ϊ��![]() ��
��
�ҵ�ƽ���ɼ�Ϊ��![]() ��
��
����ƽ���ɼ�Ϊ��![]() ��
��
��![]()
���ҵ�ƽ���ɼ���
��Ӧ��¼ȡ�ң�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪Rt��ABC�У���BAC=90����AB=AC����EΪ��ABC��һ�㣬����AE��CE��CE��AE������B��BD��AE����AE���ӳ�����D��

��1����ͼ1����֤BD=AE��
��2����ͼ2����HΪBC�е㣬�ֱ�����EH��DH������EDH�Ķ�����
��3����ͼ3���ڣ�2���������£���MΪCH�ϵ�һ�㣬����EM����FΪEM���е㣬����FH������D��DG��FH����FH���ӳ����ڵ�G����GH��FH=6��5����FHM�����Ϊ30����EHB=��BHG�����߶�EH�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
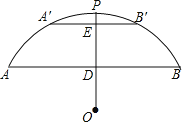
����Ŀ����ͼ����һ��������Բ���Σ����Ŀ��AB=60�ף�����PD=18�ף�
��1����Բ�����ڵ�Բ�İ뾶r�ij���
��2������ˮ���ĵ����ֻ��30��ʱ��Ҫ��ȡ������ʩ����������ˮ��ֻ��4�ף���PE=4��ʱ���Ƿ�Ҫ��ȡ������ʩ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����1�������1��������150Ԫ������2�������1��������200Ԫ.
(1)��ÿ�������ÿ��������ۼۣ�
(2)���ijУ�ƻ�������������50�����ܷ��ò�����4000Ԫ������������ٸ�����?
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̵깺���ס���������Ʒ����֪ÿ��������Ʒ�ļ۸��ÿ��������Ʒ�ļ۸��10Ԫ����350Ԫ���������Ʒ�ļ���ǡ������300Ԫ����������Ʒ�ļ�����ͬ��
��1����ס���������Ʒÿ���ļ۸���Ƕ���Ԫ?
��2���ƻ�������������Ʒ��50������Ͷ��ľ��Ѳ�����3200Ԫ����ô������ټ�������Ʒ?
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У���B��90�㣬CDΪ��ACB�Ľ�ƽ���ߣ���AC����ȡ��E��ʹDE��DB���ҡ�AED��90�㣮����A��������ACB������������

A.��AED��180�㩁������B.��AED��180�㩁����![]() ��
��
C.��AED��90�㩁��+��D.��AED��90��+��+![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABCΪ�ȱ������Σ�DΪ��BA�ӳ�����һ�㣬����CD����CDΪһ�����ȱ�������CDE������AE��
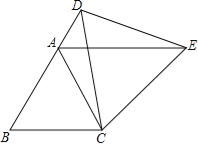
��1����֤����CBD�ա�CAE��
��2���ж�AE��BC��λ�ù�ϵ����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������״��С��ȫ��ͬ��С�����ο�Ƭ����ͼ�������ص��ķ���һ������Ϊ�����Σ���Ϊa���ף���Ϊb���ף��ĺ��ӵײ�����ͼ���������ӵ���δ����Ƭ���ǵIJ�������Ӱ��ʾ����ͼ����������Ӱ���ֵ��ܳ����ǣ� ��
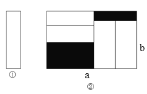
A. 4a����B. 4b����C. 2��a+b������D. 4��a-b������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����![]() ��
��![]() ��
��![]() .��
.��![]() ��
��![]() �ϣ�BC��ED�ཻ�ڵ�F��FE=FC��AB=DC��CFƽ����ACE.
�ϣ�BC��ED�ཻ�ڵ�F��FE=FC��AB=DC��CFƽ����ACE.

��1��![]() ��
��![]() �������˵�����ɣ�
�������˵�����ɣ�
��2����˵��![]() ��
��![]() ������.
������.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com