

分析 (1)根据图②、③的作法将九个数同时减0.5填到图④中相应位置,类比等式性质得出规律即可;
(2)根据图⑤、⑥的作法将九个数同时乘-2填到图⑦相应位置,可类比等式的性质得出规律;将1,2,3,4,5,6,7,8,9这9个数先乘以2、再加上1即可得出结论.
解答 解:(1)如图④,
由题意知,三阶幻方的性质(1)构成三阶幻方的九个数,每个数同时加或减同一个数,所得到的九个数仍能构成三阶幻方.
故答案为:构成三阶幻方的九个数,每个数同时加或减同一个数,所得到的九个数仍能构成三阶幻方;
(2)如图⑦,
由题意,得:三阶幻方的性质(2)构成三阶幻方的九个数,每个数同时乘同一个数或除以同一个不为0的数,所得到的九个数仍能构成三阶幻方.
故答案为:构成三阶幻方的九个数,每个数同时乘同一个数或除以同一个不为0的数,所得到的九个数仍能构成三阶幻方.
先将三阶幻方的九个数1,2,3,4,5,6,7,8,9,每个数都乘2,得2,4,6,8,10,12,14,16,18,
根据三阶幻方性质②,2,4,6,8,10,12,14,16,18能构成三阶幻方.
再将2,4,6,8,10,12,14,16,18,每个数都加1得3,5,7,9,11,13,15,17,19,
根据三阶幻方性质①,3,5,7,9,11,13,15,17,19能构成三阶幻方.
所以,3,5,7,9,11,13,15,17,19这九个数能构成三阶幻方.
点评 本题主要考查数字的变化类,理解题意类比等式的性质是解题的关键.


 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:初中数学 来源: 题型:选择题
 如图,在等边△ABC中,M,N分别在BC,AC上移动,且BM=CN,AM与BN相交于点Q,则∠BAM+∠ABN的度数是( )
如图,在等边△ABC中,M,N分别在BC,AC上移动,且BM=CN,AM与BN相交于点Q,则∠BAM+∠ABN的度数是( )| A. | 60° | B. | 55° | C. | 45° | D. | 不能确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -$\frac{12}{5}$ | B. | -$\frac{17}{5}$ | C. | -3 | D. | -4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
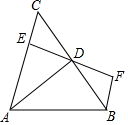 如图,AD是△ABC的角平分线,DE⊥AC,垂足为E,BF∥AC交ED的延长线于点F,若BC恰好平分∠ABF,AE=2EC,给出下列四个结论:①DE=DF;②DB=DC;③AD⊥BC;④AB=3BF,其中正确的结论共有( )
如图,AD是△ABC的角平分线,DE⊥AC,垂足为E,BF∥AC交ED的延长线于点F,若BC恰好平分∠ABF,AE=2EC,给出下列四个结论:①DE=DF;②DB=DC;③AD⊥BC;④AB=3BF,其中正确的结论共有( )| A. | ①②③ | B. | ①③④ | C. | ②③ | D. | ①②③④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com