
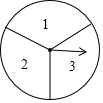
 如图,一个转盘被分成3等分,每一份上各写有一个数字,随机转动转盘2次,第一次转到的数字数字为十位数字,第二次转到的数字为个位数字,2次转动后组成一个两位数(若指针停在等分线上则重新转一次)
如图,一个转盘被分成3等分,每一份上各写有一个数字,随机转动转盘2次,第一次转到的数字数字为十位数字,第二次转到的数字为个位数字,2次转动后组成一个两位数(若指针停在等分线上则重新转一次) 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案科目:初中数学 来源: 题型:解答题
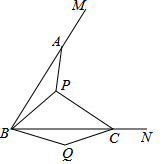 如图,已知∠MBN=60°,在BM,BN上分别截取BA=BC,P是∠MBN内的一点,连接PA,PB,PC,以BP为边作∠PBQ=60°,且BQ=BP,连接CQ.
如图,已知∠MBN=60°,在BM,BN上分别截取BA=BC,P是∠MBN内的一点,连接PA,PB,PC,以BP为边作∠PBQ=60°,且BQ=BP,连接CQ.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
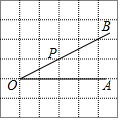 如图,点P是∠AOB的边OB上的一点,过点P画OB的垂线,交OA于点C;
如图,点P是∠AOB的边OB上的一点,过点P画OB的垂线,交OA于点C;查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com