
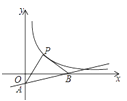
【题目】如图,直线y=![]() x﹣1与坐标轴交于A,B两点,点P是曲线y=
x﹣1与坐标轴交于A,B两点,点P是曲线y=![]() (x>0)上一点,若△PAB是以∠APB=90°的等腰三角形,则k= _________.
(x>0)上一点,若△PAB是以∠APB=90°的等腰三角形,则k= _________.
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,点![]() 在第一象限,
在第一象限,![]() 轴于
轴于![]() ,
,![]() 轴于
轴于![]() ,
,![]() ,
,![]() ,有一反比例函数图象刚好过点
,有一反比例函数图象刚好过点![]() .
.

(1)分别求出过点![]() 的反比例函数和过
的反比例函数和过![]() ,
,![]() 两点的一次函数的函数表达式;
两点的一次函数的函数表达式;
(2)直线![]() 轴,并从
轴,并从![]() 轴出发,以每秒
轴出发,以每秒![]() 个单位长度的速度向
个单位长度的速度向![]() 轴正方向运动,交反比例函数图象于点
轴正方向运动,交反比例函数图象于点![]() ,交
,交![]() 于点
于点![]() ,交直线
,交直线![]() 于点
于点![]() ,当直线
,当直线![]() 运动到经过点
运动到经过点![]() 时,停止运动.设运动时间为
时,停止运动.设运动时间为![]() (秒).
(秒).
①问:是否存在![]() 的值,使四边形
的值,使四边形![]() 为平行四边形?若存在,求出
为平行四边形?若存在,求出![]() 的值;若不存在,说明理由;
的值;若不存在,说明理由;
②若直线![]() 从
从![]() 轴出发的同时,有一动点
轴出发的同时,有一动点![]() 从点
从点![]() 出发,沿射线
出发,沿射线![]() 方向,以每秒
方向,以每秒![]() 个单位长度的速度运动.是否存在
个单位长度的速度运动.是否存在![]() 的值,使以点
的值,使以点![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形为平行四边形;若存在,求出
为顶点的四边形为平行四边形;若存在,求出![]() 的值,并进一步探究此时的四边形是否为特殊的平行四边形;若不存在,说明理由.
的值,并进一步探究此时的四边形是否为特殊的平行四边形;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一座人行天桥引桥部分的示意图,上桥通道AD∥BE,水平平台DE和地面AC平行,立柱BC和地面AC垂直,∠A=37°.已知天桥的高度BC为4.8米,引桥的水平跨度AC为8米,求水平平台DE的长度.(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某兴趣小组为了解我市气温变化情况,记录了今年月份连续![]() 天的最低气温(单位:℃):
天的最低气温(单位:℃):![]() .关于这组数据,下列结论不正确的是( )
.关于这组数据,下列结论不正确的是( )
A.平均数是![]() B.中位数是
B.中位数是![]() C.众数是
C.众数是![]() D.方差是
D.方差是![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图为一座抛物线型的拱桥,AB、CD分别表示两个不同位置的水面宽度,O为拱桥顶部,水面AB宽为10米,AB距桥顶O的高度为12.5米,水面上升2.5米到达警戒水位CD位置时,水面宽为( )米.

A. 5 B. 2![]() C. 4
C. 4![]() D. 8
D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
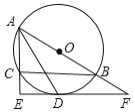
【题目】如图,![]() 是
是![]() ABC的外接圆,AB为直径,∠BAC的平分线交
ABC的外接圆,AB为直径,∠BAC的平分线交![]() 于点D,过点D作DE
于点D,过点D作DE![]() AC分别交AC、AB的延长线于点E、F.
AC分别交AC、AB的延长线于点E、F.
(1)求证:EF是![]() 的切线;
的切线;
(2)若AC=4,CE=2,求![]() 的长度.(结果保留
的长度.(结果保留![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD是BC边上的高,AE是BC边上的中线,∠C=45°,sinB=![]() ,AD=1.
,AD=1.
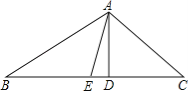
(1)求BC的长;
(2)求tan∠DAE的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
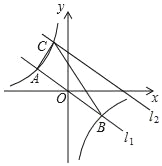
【题目】如图,在平面直角坐标系中,直线l1:y=﹣![]() x与反比例函数y=
x与反比例函数y=![]() 的图象交于A,B两点(点A在点B左侧),已知A点的纵坐标是2;
的图象交于A,B两点(点A在点B左侧),已知A点的纵坐标是2;
(1)求反比例函数的表达式;
(2)根据图象直接写出﹣![]() x>
x>![]() 的解集;
的解集;
(3)将直线l1:y=- ![]() x沿y向上平移后的直线l2与反比例函数y=
x沿y向上平移后的直线l2与反比例函数y=![]() 在第二象限内交于点C,如果△ABC的面积为30,求平移后的直线l2的函数表达式.
在第二象限内交于点C,如果△ABC的面积为30,求平移后的直线l2的函数表达式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com