
如图,在矩形ABCD中,M、N分别AD、BC的中点,P、Q分别BM、DN的中点.
(1)求证:四边形MPNQ是菱形;
(2)若AB=2,BC=4,求四边形MPNQ的面积.
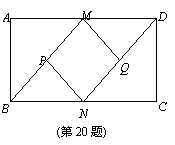 |
(1)证明:∵四边形ABCD是矩形,
∴AD=BC,AD∥BC.
连结MN,∵M、N分别AD、BC的中点,
∴MD= AD,BN=
AD,BN= BC.
BC.
∴MD=BN,MD∥BN,∴四边形BNDM是平行四边形.
∴MB=ND.
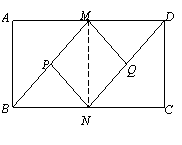 ∵P、Q分别BM、DN的中点,∴MP=
∵P、Q分别BM、DN的中点,∴MP= MB,NQ=
MB,NQ= DN.
DN.
∴MP=NQ.
又∵MP∥NQ,∴四边形MPNQ是平行四边形.
∵ABCD为矩形,M、N分别AD、BC的中点,
∴四边形ABNM为矩形,∴MN⊥BC.
∴在Rt△MNB中,PN= BM.∴PN=PM.
BM.∴PN=PM.
∴四边形MPNQ是菱形.
(2)∵AB=2,BC=4,∴MN=BN=2
∵P为MB的中点,∴PN⊥MB,PN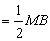
在Rt△MNB中,MB=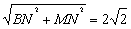 …………………5分
…………………5分
∴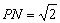 ,∴四边形MPNQ是边长为
,∴四边形MPNQ是边长为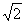 的正方形.
的正方形.
∴四边形MPNQ的面积为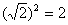 ……………………………7分
……………………………7分


 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案科目:初中数学 来源: 题型:
某批发商以40元/千克的成本价购入了某产品700千克,据市场预测,该产品的
销售价y(元/千克)与保存时间x(天)的函数关系为y=50+2x,但保存这批产品平均每天
将损耗15千克,且最多保存15天.另外,批发商每天保存该批产品的费用为50元.
(1)若批发商在保存该产品5天时一次性卖出,则可获利 元.
(2)如果批发商希望通过这批产品卖出获利10000元,则批发商应在保存该产品多少
天时一次性卖出?
查看答案和解析>>
科目:初中数学 来源: 题型:
阅读下面材料:
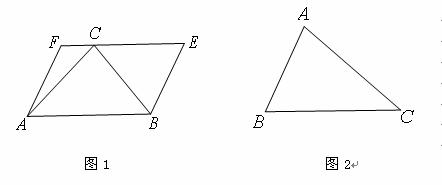
如果一个三角形和一个平行四边形满足条件:三角形的一边与平行四边形的一边重合,三角形这边所对的顶点在平行四边形这边的 对边上,则称这样的平行四边形为三角形的“友好平行四边形”.如图1 所示,平行四边形
对边上,则称这样的平行四边形为三角形的“友好平行四边形”.如图1 所示,平行四边形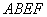 即为
即为
 的“友好平行四边形”.
的“友好平行四边形”.
请解决下列问题:
(1)仿照以上叙述,说明什么是一个三角形的“友好矩形”;
(2)若 是钝角三角形,则
是钝角三角形,则 显然只有一个“友好矩形”,
显然只有一个“友好矩形”,
若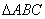 是直角三角形,其“友好矩形”有 个;
是直角三角形,其“友好矩形”有 个;
(3)若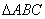 是锐角三角形,且
是锐角三角形,且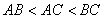 ,如图2,请画出
,如图2,请画出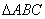 的所有“友好矩形”;指出其中周长最小的“友好矩形”并说明理由.
的所有“友好矩形”;指出其中周长最小的“友好矩形”并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com