
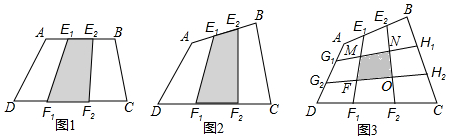
分析 (1)连接AC,AF1,E2F1,E1F2,BF2,CE2,根据三角形的面积公式得到S${\;}_{△A{E}_{2}C}$=$\frac{2}{3}$S△ABC,同理得到S${\;}_{△A{F}_{1}C}$=$\frac{2}{3}$S△ADC,计算即可;
(2)(3)根据(1)的结论计算即可.
解答 解:如图1,连接AC,AF1,E2F1,E1F2,BF2,CE2,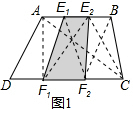
∵E1、E2是AB的三等分点,
∴AE2=$\frac{2}{3}$AB,
∴S${\;}_{△A{E}_{2}C}$=$\frac{2}{3}$S△ABC,
同理,S${\;}_{△A{F}_{1}C}$=$\frac{2}{3}$S△ADC,
∴S${\;}_{四边形A{F}_{1}C{E}_{2}}$=$\frac{2}{3}$S四边形ABCD,
∵AE1=E1E2,
∴S${\;}_{△A{F}_{1}{E}_{1}}$=S${\;}_{△{E}_{2}{F}_{1}{E}_{1}}$,
同理,四边形E1E2F2F1的面积与四边形ABCD面积的比为1:3,
故答案为:1:3;
(2)由(1)得,四边形E1E2F2F1的面积与四边形ABCD面积的比为1:3;
(3)由(1)得,四边形G1G2H2H1的面积与四边形ABCD面积的比为1:3;四边形E1E2F2F1的面积与四边形ABCD面积的比为1:3,
∴四边形MNOP的面积与四边形ABCD的面积的比为1:9,
故答案为:1:9.
点评 本题考查的是梯形的性质、三角形的面积计算,掌握等底等高的三角形面积相等是解题的关键.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:解答题
| 购苹果数 | 不超过30kg | 30kg以下但不超过50kg | 50kg以上 |
| 每千克价格 | 3元 | 2.5元 | 2元 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
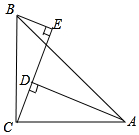 如图,在△ABC中,∠ACB=90°,AC=BC,BE⊥CE于E,AD⊥CE于D
如图,在△ABC中,∠ACB=90°,AC=BC,BE⊥CE于E,AD⊥CE于D查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,A、B两地有公路和铁路相连,在这条路上有一家食品厂,它到B地的距离是到A地的2倍,这家工厂从A地购买原料,制成食品卖到B地.已知公路运价为1.5元/(公里•吨),铁路运价为1元/(公里•吨),这两次运输(第一次:A地→食品厂,第二次:食品厂→B地)共支出公路运费15600元,铁路运费20600元.
如图,A、B两地有公路和铁路相连,在这条路上有一家食品厂,它到B地的距离是到A地的2倍,这家工厂从A地购买原料,制成食品卖到B地.已知公路运价为1.5元/(公里•吨),铁路运价为1元/(公里•吨),这两次运输(第一次:A地→食品厂,第二次:食品厂→B地)共支出公路运费15600元,铁路运费20600元.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
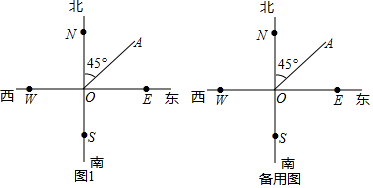
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com