
| |||||||||||
(1) |
∵菱形ABCD的周长是16. ∴AB=4(菱形四边都相等). ∵AE⊥BC且BE=EC(已知), ∴AC=AB=4(线段垂直平分线上的点到线段两端点的距离相等). ∵在菱形ABCD中,AC⊥BD且AO= ∴OA=2,BO= ∴BD=2OB= |
(2) |
知道菱形的两条对角线长,那么根据菱形的面积等于对角线乘积的一半,可求出它的面积,也可以根据底乘以高求出其面积. ∴S菱形ABCD= 说明:菱形的两条对角线把菱形分成四个全等的直角三角形,故菱形的面积有两种求法:底乘以高,或对角线相乘再除以2,要善于运用菱形的这个性质特征解决有关问题. |


科目:初中数学 来源: 题型:
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源:2011年湖南省长沙市初二上学期末数学卷 题型:解答题
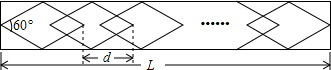
学校植物园沿路护栏纹饰部分设计成若干个相同的菱形图案,每增加一个菱形图案,纹饰长度就增加d cm,如图所示.已知每个菱形的横向对角线长为30cm.

(1)若该纹饰要231个菱形图案,试用含d的代数式表示纹饰的长度L;
当d=26时,求该纹饰的长度L;
(2)当d=20时,若保持(1)中纹饰长度不变,则需要多少个这样的菱形图案?
查看答案和解析>>
科目:初中数学 来源:2010-2011学年南京市考数学一模试卷 题型:填空题
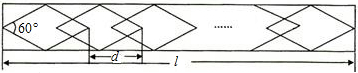
学校植物园沿路护栏纹饰部分设计成若干个全等菱形图案,每增加一个菱形图案,纹饰长度就增加dcm,如图所示.已知每个菱形图案的边长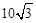 cm,其一个内角为60°,若纹饰的总长度L=5030 cm,当d=20时,则需要 个这样的菱形图案.
cm,其一个内角为60°,若纹饰的总长度L=5030 cm,当d=20时,则需要 个这样的菱形图案.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com