

 得到BC=CD•tan∠BDC=0.34x,在Rt△ACD中利用tan∠ADC=
得到BC=CD•tan∠BDC=0.34x,在Rt△ACD中利用tan∠ADC= ,得到AC=CD•tan∠ADC=2.1x,则AB=AC-BC,列方程可得2=2.1x-0.34x,解得x的值即可.
,得到AC=CD•tan∠ADC=2.1x,则AB=AC-BC,列方程可得2=2.1x-0.34x,解得x的值即可.


科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
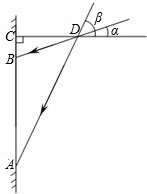 在一次课题学习课上,同学们为教室窗户设计一个遮阳蓬,小明同学绘制的设计图如图所示,其中,AB表示窗户,且AB=2米,BCD表示直角遮阳蓬,已知当地一年中在午时的太阳光与水平线CD的最小夹角α为18.6°,最大夹角β为64.5度.请你根据以上数据,帮助小明同学计算出遮阳蓬中CD的长是多少米?(结果保留两个有效数字)
在一次课题学习课上,同学们为教室窗户设计一个遮阳蓬,小明同学绘制的设计图如图所示,其中,AB表示窗户,且AB=2米,BCD表示直角遮阳蓬,已知当地一年中在午时的太阳光与水平线CD的最小夹角α为18.6°,最大夹角β为64.5度.请你根据以上数据,帮助小明同学计算出遮阳蓬中CD的长是多少米?(结果保留两个有效数字)查看答案和解析>>
科目:初中数学 来源:2012-2013学年江西省景德镇市八年级下学期期末质量检测数学试卷(带解析) 题型:解答题
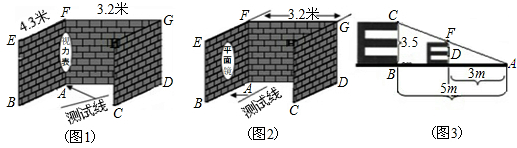
为了加强视力保护意识,小明想在长为3.2米,宽为4.3米的书房里挂一张测试距离为5米的视力表.在一次课题学习课上,小明向全班同学征集“解决空间过小,如何放置视力表问题”的方案,其中甲、乙、丙三位同学设计方案新颖,构思巧妙.
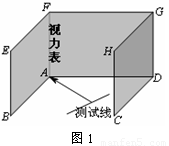
(1)甲生的方案:如下页图1,将视力表挂在墙ABEF和墙ADGF的夹角处(不考虑视力表与墙角AF之间的距离),被测试人站立在对角线AC上,问:甲生的设计方案是否可行?请说明理由.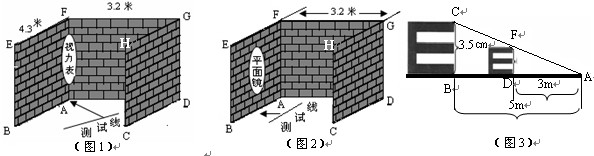
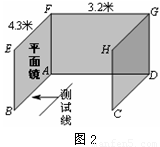
(2)乙生的方案:如图2,将视力表挂在墙CDGH上,在墙ABEF上挂一面足够大的平面镜,根据平面镜成像原理可计算得到:测试线应画在距离墙ABEF 米处.
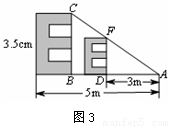
(3)丙生的方案:如图3,根据测试距离为5m的大视力表制作一个测试距 为3m的小视力表.如果大视力表中“E”的长是3.5cm,那么小视力表中相应“E”的长是多少cm?
查看答案和解析>>
科目:初中数学 来源:2014届河南省郑州市八年级第二学期期末考试数学试卷(解析版) 题型:解答题
为了加强视力保护意识,小明想在长为4.3米,宽为3.2米的书房里挂一张测试距离为5米的视力表.在一次课题学习课上,小明向全班同学征集“解决空间过小,如何放置视力表问题”的方案,其中甲、乙、丙三位同学设计的方案新颖,构思巧妙.
(1)甲生的方案:如图1,将视力表挂在墙ABEF和墙ADGF的夹角处,被测试人站立在对角线AC上,问:甲生的设计方案是否可行?请说明理由.
(2)乙生的方案:如图2,将视力表挂在墙CDGH上,在墙ABEF上挂一面足够大的平面镜,根据平面镜成像原理课计算得到:测试线应画在距离墙ABEF 米处.
(3)丙生的方案:如图3,根据测试距离为5m的大视力表制作一个测试距离为3m的小视力表.图中的△ADF∽△ABC,如果大视力表中“E”的长是3.5cm,那么小视力表中相应的“E”的长是多少cm?
查看答案和解析>>
科目:初中数学 来源:2014届江西省景德镇市八年级下学期期末质量检测数学试卷(解析版) 题型:解答题
为了加强视力保护意识,小明想在长为3.2米,宽为4.3米的书房里挂一张测试距离为5米的视力表.在一次课题学习课上,小明向全班同学征集“解决空间过小,如何放置视力表问题”的方案,其中甲、乙、丙三位同学设计方案新颖,构思巧妙.
(1)甲生的方案:如下页图1,将视力表挂在墙ABEF和墙ADGF的夹角处(不考虑视力表与墙角AF之间的距离),被测试人站立在对角线AC上,问:甲生的设计方案是否可行?请说明理由.
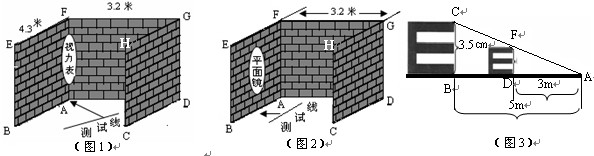
(2)乙生的方案:如图2,将视力表挂在墙CDGH上,在墙ABEF上挂一面足够大的平面镜,根据平面镜成像原理可计算得到:测试线应画在距离墙ABEF 米处.
(3)丙生的方案:如图3,根据测试距离为5m的大视力表制作一个测试距 为3m的小视力表.如果大视力表中“E”的长是3.5cm,那么小视力表中相应“E”的长是多少cm?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com