
 已知实数a、b在数轴上的位置如图所示,试化简:$\frac{a}{a-b}$$\sqrt{\frac{{a}^{2}b-2a{b}^{2}+{b}^{3}}{a}}$.
已知实数a、b在数轴上的位置如图所示,试化简:$\frac{a}{a-b}$$\sqrt{\frac{{a}^{2}b-2a{b}^{2}+{b}^{3}}{a}}$. 分析 利用实数在数轴的位置判断a,b,a-b的符号,再进一步化简合并即可.
解答 解:∵根据数轴可知:b>a>0,
∴a-b<0,
∴$\frac{a}{a-b}$$\sqrt{\frac{{a}^{2}b-2a{b}^{2}+{b}^{3}}{a}}$
=$\frac{a}{a-b}$$\sqrt{\frac{b({a}^{2}-2ab+{b}^{2})}{a}}$
=$\frac{a}{a-b}$$\frac{\sqrt{ab(a-b)^{2}}}{a}$
=$\frac{a}{a-b}$$\frac{-(a-b)\sqrt{ab}}{a}$
=-$\sqrt{ab}$.
点评 此题考查实数与数轴,绝对值的意义,二次根式的化简,正确判定字母与算式符号是解决问题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
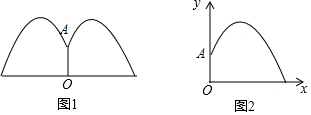 公园里有一个圆形喷水池,在水池中央垂直于水面安装一个花形柱子OA,O恰好在水面中心,布置在柱子顶端A处的喷头向外喷水,水流在各个方向上沿形状相同的抛物线路径落下,且在过OA任意平面上的抛物线如图1所示,建立直角坐标系如图2,水流喷出的高度(m)与水面距离x(m)之间的函数关系式是y=a(x-h)2+k,且OA=1.25m,水柱在离OA为1m处到时达最大高度2.25m,请回答下列问题:
公园里有一个圆形喷水池,在水池中央垂直于水面安装一个花形柱子OA,O恰好在水面中心,布置在柱子顶端A处的喷头向外喷水,水流在各个方向上沿形状相同的抛物线路径落下,且在过OA任意平面上的抛物线如图1所示,建立直角坐标系如图2,水流喷出的高度(m)与水面距离x(m)之间的函数关系式是y=a(x-h)2+k,且OA=1.25m,水柱在离OA为1m处到时达最大高度2.25m,请回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com