
【题目】如图,某山顶上建有手机信号中转塔AB,在地面D处测得塔尖的仰角∠ADC=60°,塔底的仰角∠BDC=45°,点D距离塔AB所在直线的距离DC为100米,求手机信号中转塔AB的高度(参考数据: ![]() ≈1.414,
≈1.414, ![]() ≈1.732,结果保留整数).
≈1.732,结果保留整数). 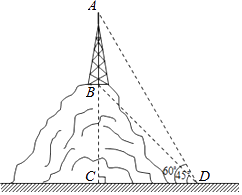
【答案】解:由题意可知,△ACD与△BCD都是直角三角形.
在Rt△BCD中,∵∠BDC=45°,
∴BC=CD=100米.
在Rt△ACD中,∵∠ADC=60°,CD=100米,
∴tan∠ADC= ![]() ,即
,即 ![]() =
= ![]() ,
,
∴AC=100 ![]() ,
,
∴AB=AC﹣BC=100( ![]() ﹣1)≈73(米).
﹣1)≈73(米).
答:手机信号中转塔的高度约为73米
【解析】先在Rt△BCD中,根据∠BDC=45°,得出BC=CD=100;再在Rt△ACD中,根据正切函数的定义,求出AC=100 ![]() ,然后由AB=AC﹣BC即可求解.
,然后由AB=AC﹣BC即可求解.
【考点精析】本题主要考查了关于仰角俯角问题的相关知识点,需要掌握仰角:视线在水平线上方的角;俯角:视线在水平线下方的角才能正确解答此题.


 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案科目:初中数学 来源: 题型:
【题目】如图的△ABC中有一正方形DEFG,其中D在AC上,E、F在AB上,直线AG分别交DE、BC于M、N两点.若∠B=90°,AB=4,BC=3,EF=1,则BN的长度为何?( ) 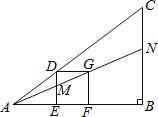
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】勾股定理是一条古老的数学定理,它有很多种证明方法,我国汉代数学家赵爽根据弦图,利用面积进行了证明.著名数学家华罗庚提出把“数形关系”(勾股定理)带到其他星球,作为地球人与其他星球“人”进行第一次“谈话”的语言.
请根据图1中直角三角形叙述勾股定理.

以图1中的直角三角形为基础,可以构造出以a,b为底,以a+b为高的直角梯形(如图2).请你利用图2,验证勾股定理;
利用图2中的直角梯形,我们可以证明![]() .其证明步骤如下:
.其证明步骤如下:
∵BC=a+b,AD=_____;
又∵在直角梯形ABCD中有BC_____AD(填大小关系),即_____.
∴![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,∠A=60°,点D是线段BC的中点,∠EDF=120°,DE与线段AB相交于点E,DF与线段AC(或AC的延长线)相交于点F.
(1)如图1,若DF⊥AC,垂足为F,AB=4,求BE的长;
(2)如图2,将(1)中的∠EDF绕点D顺时针旋转一定的角度,DF仍与线段AC相交于点F.求证:BE+CF= ![]() AB.
AB.
(3)如图3,若∠EDF的两边分别交AB,AC的延长线于E、F两点,(2)中的结论还成立吗?如果成立,请证明;如果不成立,请直接写出线段BE,AB,CF之间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,△ABC中,CD⊥AB于D,且BD : AD : CD=2 : 3 : 4,
(1)求证:AB=AC;
(2)已知S△ABC=40cm2,如图2,动点M从点B出发以每秒1cm的速度沿线段BA向点A 运动,同时动点N从点A出发以相同速度沿线段AC向点C运动,当其中一点到达终点时整个运动都停止. 设点M运动的时间为t(秒),
①若△DMN的边与BC平行,求t的值;
②若点E是边AC的中点,问在点M运动的过程中,△MDE能否成为等腰三角形?若能,求出t的值;若不能,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将Rt△ABC绕直角顶点顺时针旋转90°,得到△A′B′C′,连接AA′,若∠1=22°,则∠B的度数是( ) 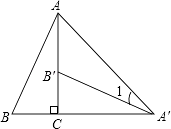
A.67°
B.62°
C.82°
D.72°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“龟兔首次赛跑”之后,输了比赛的兔子没有气馁,总结反思后,和乌龟约定再赛一场.图中的函数图象刻画了“龟兔再次赛跑”的故事(x表示乌龟从起点出发所行的时间,y1表示乌龟所行的路程,y2表示兔子所行的路程).有下列说法:
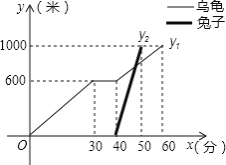
①兔子和乌龟同时从起点出发;
②“龟兔再次赛跑”的路程为1000米;
③乌龟在途中休息了10分钟;
④兔子在途中750米处追上乌龟.
其中正确的说法共有____________个.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:有一个直角三角形ABC,∠C=90°,AC=10,BC=5,一条线段PQ=AB,P、Q两点分别在AC和过点A且垂直于AC的射线AX上运动,问P点运动到离A的距离等于___________时,ΔABC和ΔPQA全等.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com