
 x2经过AD的中点M.
x2经过AD的中点M.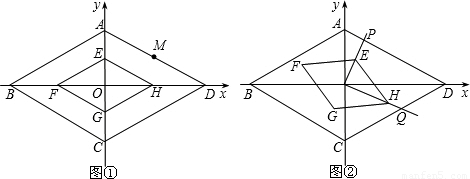
 x2经过AD的中点M,设M的坐标为(x,
x2经过AD的中点M,设M的坐标为(x, x2),由于∠BAD=120°,易知∠OAD=60°,因此
x2),由于∠BAD=120°,易知∠OAD=60°,因此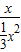 =
=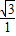 ,解得x=
,解得x=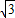 ,x=0(舍去).因此M点的坐标为(
,x=0(舍去).因此M点的坐标为(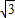 ,1).也就能得出A点的坐标为(0,2),D点的坐标为(2
,1).也就能得出A点的坐标为(0,2),D点的坐标为(2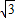 ,0).
,0). AD,已知两菱形的位似比为2:1,因此EF=
AD,已知两菱形的位似比为2:1,因此EF= AD,也就是EF=AP,由此可得出当α=60°时,AP∥=EF,即四边形APEF是平行四边形.
AD,也就是EF=AP,由此可得出当α=60°时,AP∥=EF,即四边形APEF是平行四边形.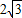 ,0).
,0).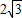 ,菱形ABCD边长为4,∠BAO=60°
,菱形ABCD边长为4,∠BAO=60° AD=2,∠FEO=60°
AD=2,∠FEO=60°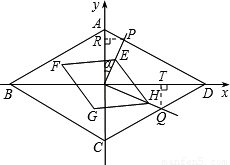 设TQ=y,
设TQ=y,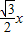 ,
, x,
x,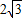 -TQ•tan60°=2
-TQ•tan60°=2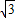 -
-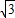 y
y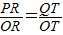
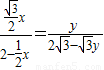 ,
,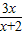
 ×2
×2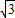 (2-
(2- x)+
x)+ ×2
×2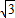 ×
×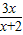
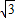 -
-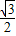 x+
x+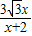 .
.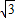 -
-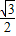 x+
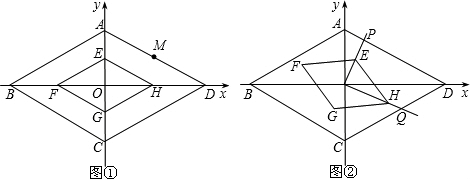
x+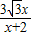 .(0<x<4)
.(0<x<4)

科目:初中数学 来源: 题型:
| 1 | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 (2012•南昌)如图,已知两个菱形ABCD、CEFG,其中点A、C、F在同一直线上,连接BE、DG.
(2012•南昌)如图,已知两个菱形ABCD、CEFG,其中点A、C、F在同一直线上,连接BE、DG.查看答案和解析>>
科目:初中数学 来源:2012年初中毕业升学考试(江西卷)数学(带解析) 题型:解答题
如图,已知两个菱形ABCD.CEFG,其中点A.C.F在同一直线上,连接BE、DG.
(1)在不添加辅助线时,写出其中的两对全等三角形;
(2)证明:BE=DG.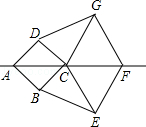
查看答案和解析>>
科目:初中数学 来源:2012年初中毕业升学考试(江西卷)数学(解析版) 题型:解答题
如图,已知两个菱形ABCD.CEFG,其中点A.C.F在同一直线上,连接BE、DG.
(1)在不添加辅助线时,写出其中的两对全等三角形;
(2)证明:BE=DG.
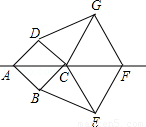
查看答案和解析>>
科目:初中数学 来源:2009年湖北省荆州市中考数学试卷(解析版) 题型:解答题
 x2经过AD的中点M.
x2经过AD的中点M.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com