
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���A��B������ֱ��ǣ���3��0������0��6��������P�ӵ�O��������x����������ÿ��1����λ���ٶ��˶���ͬʱ����C�ӵ�B������������BO������ÿ��2����λ���ٶ��˶�����CP��COΪ�ڱ߹���PCOD�����߶�OP�ӳ�����ȡ��E��ʹPE=AO�����P�˶���ʱ��Ϊt�룮

��1������C�˶����߶�OB���е�ʱ����t��ֵ����E�����ꣻ
��2������C���߶�OB��ʱ����֤���ı���ADECΪƽ���ı��Σ�
��3�����߶�PE��ȡ��F��ʹPF=2������F��MN��PE����ȡFM=![]() ��FN=1���ҵ�M��N�ֱ��ڵ�һ�������ޣ����˶������У�����M��N�У���һ�������ı���ADEC�ı���ʱ��ֱ��д����������������t��ֵ��
��FN=1���ҵ�M��N�ֱ��ڵ�һ�������ޣ����˶������У�����M��N�У���һ�������ı���ADEC�ı���ʱ��ֱ��д����������������t��ֵ��
���𰸡���1����![]() ��0���� ��2��֤����������3��t1=21-12
��0���� ��2��֤����������3��t1=21-12![]() ��t2=1.5��t3=3+
��t2=1.5��t3=3+![]() ��t4=9��
��t4=9��
�������������������1����C��OB���е����ʱ�䣬�������E�����ꣻ
��2������CD��OP�ڵ�G����PCOD�ĶԽ�����ȣ����ı���ADEC��ƽ���ı��Σ�
��3�����ô���ϵ�������CE��DE�Ľ���ʽ��Ȼ����t��ʾ��M��N�����꣬�������ʽ�������t��ֵ��
���������
��1��BC=![]() OC=3����t=
OC=3����t=![]() ��
��
OP=![]() ����OE=OP+PE=OP+OA=
����OE=OP+PE=OP+OA=![]() +3=
+3=![]() ��
��
��E�������ǣ�![]() ��0����
��0����
��2������CD��OP�ڵ�G����ͼ��ʾ��
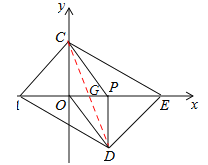
��![]() PCOD��CG=DG��OG=PG��
PCOD��CG=DG��OG=PG��
��AO=PO����AG=EG .
���ı���ADEC��ƽ���ı��Σ�
��3��C�������ǣ�0��6��2t����P�������ǣ�t��0����
��F�������ǣ�t+2��0������E�������ǣ�t+3��0����D�������ǣ�t��2t��6����
��CE�Ľ���ʽ��y=kx+b��
��![]() ��
��
��ã�  ��
��
��CE�Ľ���ʽ��y=![]() x+��6-2t����
x+��6-2t����
ͬ��DE�Ľ���ʽ��y=![]() ��
��
��M��CE��ʱ��M�������ǣ�t+2�� ![]() ����
����
��![]() ��
��
��ã�t=21��12![]() ����t=1.5��
����t=1.5��
��N��DE���ǣ�N�������ǣ�t+2����1������![]() =��1��
=��1��
��ã�t=3+![]() ��t=9��
��t=9��
��֮��t1=21-12![]() ��t2=1.5��t3=3+
��t2=1.5��t3=3+![]() ��t4=9��
��t4=9��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����м�����ȷ���ǣ�������
A. a3+a2=a5 B. a3a2=a6 C. a6��a3=a2 D. ����a2��3=��a6
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
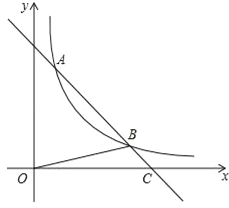
����Ŀ����ͼ��ֱ��y=��x+5��˫����![]() ��x��0���ཻ��A��B���㣬��x���ཻ��C�㣬��BOC�������
��x��0���ཻ��A��B���㣬��x���ཻ��C�㣬��BOC�������![]() ������ֱ��y=��x+5����ƽ��1����λ��������ֱ����˫����
������ֱ��y=��x+5����ƽ��1����λ��������ֱ����˫����![]() ��x��0���Ľ����У� ��
��x��0���Ľ����У� ��
A��0�� B��1�� C��2�� D��0������1������2��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪![]() . ��֤��CD��EF.����ղ��ں���������������ɣ�
. ��֤��CD��EF.����ղ��ں���������������ɣ�
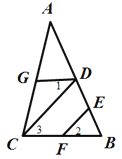
֤�����ߡ�AGD=��ACB
��DG��___________ (__________)
���3=__________ ��_____________��
�ߡ�1=��2 ��___________________��
���3=__________ ��___________________��
��__________��___________ ��__________________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ʽ�Ĵ���������ʽ�����________��Ĵ����������������ʽ�Ĵ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������һ�κ����У�y��x�������С���ǣ� ��
A. y=3x B. y=3x��2 C. y=3x+2x D. y=��3x��2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
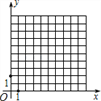
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���P��ԭ��O������ÿ������ƽ��2����λ���Ȼ�����ƽ��1����λ���ȣ�
��1��ʵ�������
��ƽ��ֱ������ϵ�������P�ӵ�O������ƽ��1�κ�2�κ�3�κ���ܵ���ĵ㣬������Ӧ���������д�ڱ����У�
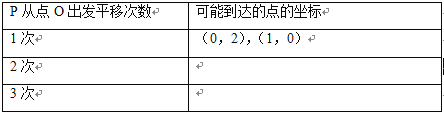
��2���۲췢�֣�
���P��x��y������һ��ƽ�ƣ���P���ܵ���ĵ���ݡ������궼����һ���Ĺ�ϵʽ.
���磺ƽ��1�κ�2x+y= _________��ƽ��2�κ�2x+y= ��ƽ��3�κ�2x+y= �������ɴ�����֪����ƽ��n�κ��P�����궼����һ���Ĺ�ϵʽ�� ��
��3��̽�����ã�
��P�ӵ�O��������n��ƽ�ƺ��Q������Q��������Ⱥ������6������Pƽ�Ƶ�·������С��50��������56����ֱ��д��Q�����꣮
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com