
【题目】如图,在△ABC中,AB=AC,点D在BC上,BD=DC,过点D作DE⊥AC,垂足为E,⊙O经过A,B,D三点.
(1)求证:AB是⊙O的直径;
(2)判断DE与⊙O的位置关系,并加以证明;
(3)若⊙O的半径为3,∠BAC=60°,求DE的长.

【答案】(1)证明见解析;(2)DE与圆O相切;(3)![]() .
.
【解析】试题分析:(1)连接AD,根据等腰三角形三线合一性质得到AD⊥BC,再根据90°的圆周角所对的弦为直径即可证得AB是⊙O的直径;(2)DE与圆O相切,理由为:连接OD,利用中位线定理得到OD∥AC,利用两直线平行内错角相等得到∠ODE为直角,再由OD为半径,即可得证;(3)由AB=AC,且∠BAC=60°,得到DABC为等边三角形,连接BF,DE为DCBF中位线,求出BF的长,即可确定出DE的长.
试题解析:(1)证明:连接AD,∵AB=AC,BD=DC,∴AD⊥BC,∴∠ADB=90°,∴AB为⊙O的直径;(2)DE与⊙O相切,理由为:连接OD,∵O、D分别为AB、BC的中点,∴OD为△ABC的中位线,∴OD∥BC,∵DE⊥BC,∴DE⊥OD,∵OD为⊙O的半径,∴DE与⊙O相切;(3)解:连接BF,∵AB=AC,∠BAC=60°,∴△ABC为等边三角形,∴AB=AC=BC=6,∵AB为⊙O的直径,∴∠AFB=∠DEC=90°,∴AF=CF=3,DE∥BF,∵D为BC中点,∴E为CF中点,DE=![]() BF,在Rt△ABF中,∠AFB=90°,AB=6,AF=3,∴BF=
BF,在Rt△ABF中,∠AFB=90°,AB=6,AF=3,∴BF=![]() ,则DE=
,则DE=![]() BF=
BF=![]() .
.



 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】把前2017个数1,2,3,…,2017的每一个数的前面任意填上“+”号或“﹣”号,然后将它们相加,则所得之结果为( )
A. 正数 B. 奇数 C. 偶数 D. 有时为奇数;有时为偶数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若A(x1,y1)、B(x2,y2)是一次函数y=ax+x﹣2图象上的不同的两点,记m=(x1﹣x2)( y1﹣y2),则当m<0时,a的取值范围是( )
A. a<0 B. a>0 C. a<﹣1 D. a>﹣1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】三角形中一个内角α是另一个内角β的两倍时,我们称此三角形为“特征三角形”,其中α称为“特征角”,如果一个“特征三角形”的“特征角”为110°,那么这个“特征三角形”的最小内角的度数为°.
查看答案和解析>>
科目:初中数学 来源: 题型:
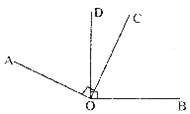
【题目】如图,若AO⊥OC,BO⊥DO,
(1)若∠DOC=38°,则∠AOB是多少度?
(2)图中有哪些角相等?
(3)若∠AOB=156°,则∠DOC是多少度?
(4)∠AOD、∠DOC、∠COB能否相等,若相等,请求出它们的度数;若不相等,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com