
【题目】如图,点![]() ,点
,点![]() ,…点
,…点![]() 在函数
在函数![]() 的图象上,
的图象上, ![]() 都是等腰直角三角形,斜边
都是等腰直角三角形,斜边![]() 都在
都在![]() 轴上(
轴上(![]() 是大于或等于2的正数数),则
是大于或等于2的正数数),则![]() __________.(用含
__________.(用含![]() 的式子表示)
的式子表示)
【答案】![]()
【解析】
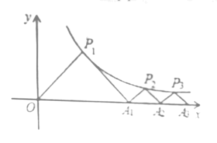
过过点P1作P1E⊥x轴于点E,过点P2作P2F⊥x轴于点F,过点P3作P3G⊥x轴于点G,,根据△P1OA1,△P2A1A2,△P3A2A3都是等腰直角三角形,可求出A1,A2,A3的横坐标,从而总结出一般规律得出点An的坐标,再求![]() 的值即可.
的值即可.
解:过点P1作P1E⊥x轴于点E,过点P2作P2F⊥x轴于点F,过点P3作P3G⊥x轴于点G,
∵△P1OA1是等腰直角三角形,
∴P1E=OE=A1E,
设点P1的坐标为(a,a),(a>0),
将点P1(a,a)代入![]() ,可得a=3,
,可得a=3,
故点A1的坐标为(6,0),
设点P2的纵坐标为b,则P2的横坐标为6+b,
将点(b+6,b)代入![]() ,可得b=
,可得b=![]() ,
,
故点A2的横坐标为![]() ,
,
同理可以得到A3的横坐标是![]() ,
,
An的横坐标是![]() ,
,
根据等腰三角形的性质得到![]() An的横坐标的一半,
An的横坐标的一半,
∴![]()
![]() .
.
故答案为:![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
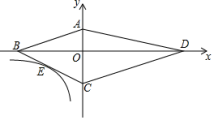
【题目】如图,四边形ABCD的顶点都在坐标轴上,若AB∥CD,![]() AOB与
AOB与![]() COD面积分别为8和18,若双曲线y=
COD面积分别为8和18,若双曲线y=![]() 恰好经过BC的中点E,则k的值为_____.
恰好经过BC的中点E,则k的值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
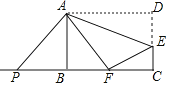
【题目】如图,矩形ABCD中,AB=12,AD=15,E是CD上的点,将△ADE沿折痕AE折叠,使点D落在BC边上点F处,点P是线段CB延长线上的动点,连接PA,若△PAF是等腰三角形,则PB的长为____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“食品安全”受到全社会的广泛关注,育才中学对部分学生就食品安全知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了下面的两幅尚不完整的统计图,请你根据统计图中所提供的信息解答下列问题:

(1)接受问卷调查的学生共有________人,扇形统计图中“基本了解”部分所对应扇形的圆心角为_________![]() ;
;
(2)请补全条形统计图;
(3)若对食品安全知识达到“了解”程度的学生中,男、女生的比例恰为![]() ,现从中随机抽取
,现从中随机抽取![]() 人参加食品安全知识竞赛,则恰好抽到
人参加食品安全知识竞赛,则恰好抽到![]() 个男生和
个男生和![]() 个女生的概率________.
个女生的概率________.
查看答案和解析>>
科目:初中数学 来源: 题型:
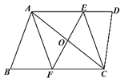
【题目】如图,在四边形ABCD中,AD∥BC,点O是对角线AC的中点,过点O作AC的垂线,分别交AD、BC于点E、F,连接AF、CE.试判断四边形AECF的形状,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx﹣3(a≠0)与x轴交于点A(﹣2,0)、B(4,0)两点,与y轴交于点C.
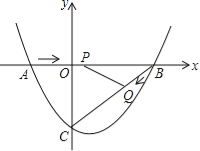
(1)求抛物线的解析式;
(2)点P从A点出发,在线段AB上以每秒3个单位长度的速度向B点运动,同时点Q从B点出发,在线段BC上以每秒1个单位长度的速度向C点运动,其中一个点到达终点时,另一个点也停止运动,当△PBQ存在时,求运动多少秒使△PBQ的面积最大,最大面积是多少?
(3)当△PBQ的面积最大时,在BC下方的抛物线上存在点K,使S△CBK:S△PBQ=5:2,求K点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】清代《修武县志》有胜果寺的记载,“康熙五十二年三月十七日,塔顶现青白二气如云,越二日乃止”,此文中的塔即为“胜果寺塔”,是修武作为“千年古县”的标志性古建筑.为了测量塔的高度,某校数学兴趣小组的两名同学采用了如下方式进行测量.如图,小明站在![]() 处,眼睛
处,眼睛![]() 距离地面的高度为
距离地面的高度为![]() ,测得塔顶
,测得塔顶![]() 的仰角为
的仰角为![]() ,小红站在距离小明
,小红站在距离小明![]() 的
的![]() 处,眼睛
处,眼睛![]() 距离地面的高度为
距离地面的高度为![]() ,测得塔顶
,测得塔顶![]() 的仰角为
的仰角为![]() ,已知
,已知![]() ,
,![]() ,塔底
,塔底![]() 在同一水平面上,由此即可求出塔高
在同一水平面上,由此即可求出塔高![]() .你知道是怎么求的吗?请写出解题过程.(结果精确到
.你知道是怎么求的吗?请写出解题过程.(结果精确到![]() .参考数据:
.参考数据:![]() )
)
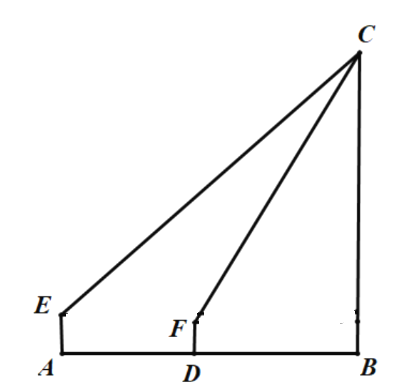
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() 为边
为边![]() 的中点.点
的中点.点![]() 从点
从点![]() 出发,以每秒
出发,以每秒![]() 个单位长度的速度沿
个单位长度的速度沿![]() 运动到点
运动到点![]() 停止,同时点
停止,同时点![]() 从点
从点![]() 出发,以每秒
出发,以每秒![]() 个单位长度的速度沿折线
个单位长度的速度沿折线![]() 运动到点
运动到点![]() 停止,当点
停止,当点![]() 停止运动时,点
停止运动时,点![]() 也停止运动.当点
也停止运动.当点![]() 不与
不与![]() 的顶点重合时,过点
的顶点重合时,过点![]() 作
作![]() 交
交![]() 的边于点
的边于点![]() 以
以![]() 和
和![]() 为边作
为边作![]() ,设点
,设点![]() 的运动时间为
的运动时间为![]() (秒),
(秒),![]() 的面积为
的面积为![]() (平方单位).
(平方单位).
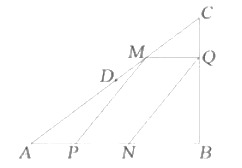
(1)当点![]() 与点
与点![]() 重合时,求
重合时,求![]() 的值;
的值;
(2)用含![]() 的代数式表示
的代数式表示![]() 的长;
的长;
(3)求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(4)连结![]() 直接写出
直接写出![]() 将
将![]() 分成面积相等的两部分时
分成面积相等的两部分时![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面直角坐标系中,抛物线C1:y1=x2-2mx+2m2-1,抛物线C2:y2=x2-2nx+2n2-1,
(1)若m=2,过点A(0,7)作直线l垂直于y轴交抛物线C1于点B、C两点.
①求BC的长;
②若抛物线C2与直线l交于点E、F两点,若EF长大于BC的长,直接写出n的范围;
(2)若m+n=k(k是常数),
①若![]() ,试说明抛物线C1与抛物线C2的交点始终在定直线上;
,试说明抛物线C1与抛物线C2的交点始终在定直线上;
②求y1+y2的最小值(用含k的代数式表示) .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com