
 .
. .
.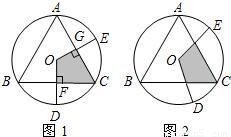
 S△ABC,易证SOFCG=
S△ABC,易证SOFCG= S△ABC.
S△ABC.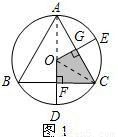 证明:(1)如图1,连接OA,OC;
证明:(1)如图1,连接OA,OC; S△ABC,
S△ABC, S△ABC.
S△ABC.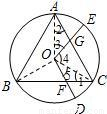
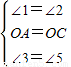 ,
, S△ABC;
S△ABC;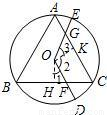 设OD交BC于点F,OE交AC于点G;
设OD交BC于点F,OE交AC于点G; S△ABC.
S△ABC.

 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:初中数学 来源:2011年山东省中考数学模拟试卷(七)(解析版) 题型:解答题
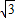 ≈1.732,
≈1.732,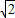 ≈1.414)
≈1.414)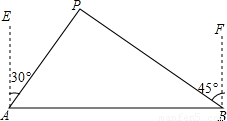
查看答案和解析>>
科目:初中数学 来源:2011年山东省济宁市曲阜市实验中学九年级数学第一次摸底试卷(解析版) 题型:填空题

查看答案和解析>>
科目:初中数学 来源:2011年山东省潍坊市中考数学模拟试卷(一)(解析版) 题型:解答题
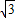 ≈1.732,
≈1.732,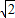 ≈1.414)
≈1.414)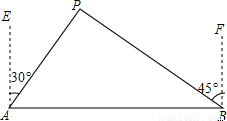
查看答案和解析>>
科目:初中数学 来源:2011年浙江省杭州市中考数学模拟试卷(39)(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com