
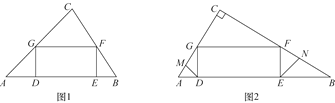
【题目】在面积为24的△ABC中,矩形DEFG的边DE在AB上运动,点F,G分别在边BC,AC上.
(1)若AB=8,DE=2EF,求GF的长;
(2)若![]() ,如图2,线段DM,EN分别为△ADG和△BEF的角平分线,求证:MG=NF;
,如图2,线段DM,EN分别为△ADG和△BEF的角平分线,求证:MG=NF;
(3)求出矩形DEFG的面积的最大值.
【答案】(1)GF的长为4.8;(2)证明见解析;(3)矩形DEFG的面积的最大值为12.
【解析】解:(1)∵△ABC的面积为24,AB=8,
∴△ABC边AB上的高h=6. 1分
设EF=x,则GF=DE=2x.
∵GF∥AB,∴△CGF∽△CAB,
∴![]() 即
即![]() 解得x=2.4. 3分
解得x=2.4. 3分
∴GF=4.8. 4分
(2)过点G作GP∥BC,过点D作DP∥EN,GP,DP交于点P,在DM的延长线上截取DQ=DP,连接QG.
∵DP∥EN,
∴![]()
又∵![]() ,∴
,∴![]() .
.
同理可得![]() .
.
又∵GD=FE,∴△GPD≌△FNE,∴![]() . 6分
. 6分
∵![]() ,∴△GQD≌△GPD,∴
,∴△GQD≌△GPD,∴![]() . 7分
. 7分
∵![]() ,∴
,∴![]() .
.
又∵![]() ,∴
,∴![]() . 9分
. 9分
∴MG=QG.
∴MG=NF. 10分
(3)作![]() 于点H,交GF于点I.
于点H,交GF于点I.
设AB=a,AB边上的高为h,DG=y,GF=x,则CH=h,CI=h-y,ah=48.
由(1)知,△CGF∽△CAB,
∴![]() 即
即![]()
则xh![]() 12分
12分
则矩形DEFG的面积![]() 即
即![]() .
.
由二次函数的有关性质知,当![]() 时,S取得最大值为
时,S取得最大值为![]() .
.
∴矩形DEFG的面积的最大值为12. 14分


科目:初中数学 来源: 题型:
【题目】已知:线段 ![]() ,
, ![]() ,
, ![]() . 求作:矩形
. 求作:矩形 ![]() .
.
以下是甲、乙两同学的作业:
甲:① 以点 ![]() 为圆心,
为圆心, ![]() 长为半径作弧;
长为半径作弧;
② 以点 ![]() 为圆心,
为圆心, ![]() 长为半径作弧;
长为半径作弧;
③ 两弧在 ![]() 上方交于点
上方交于点 ![]() ,连接
,连接 ![]() ,
, ![]() .
.
四边形 ![]() 即为所求矩形.(如图)
即为所求矩形.(如图)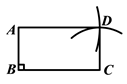
乙:① 连接 ![]() ,作线段
,作线段 ![]() 的垂直平分线,交
的垂直平分线,交 ![]() 于点
于点 ![]() ;
;
② 连接 ![]() 并延长,在延长线上取一点
并延长,在延长线上取一点 ![]() ,使
,使 ![]() ,连接
,连接 ![]() ,
, ![]() .
.
四边形 ![]() 即为所求矩形.(如图)
即为所求矩形.(如图)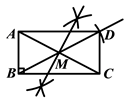
老师说甲、乙同学的作图都正确.
则甲的作图依据是:;
乙的作图依据是:.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中, ![]() ,
, ![]() 的垂直平分线分别与
的垂直平分线分别与![]() ,
, ![]() 及
及![]() 的延长线相交于点
的延长线相交于点![]() ,
, ![]() ,
, ![]() ,且
,且![]() . ⊙O是
. ⊙O是![]() 的外接圆,
的外接圆, ![]() 的平分线交
的平分线交![]() 于点
于点![]() ,交⊙O于点
,交⊙O于点![]() ,连接
,连接![]() ,
, ![]() .
.
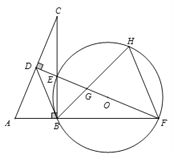
(1)求证: ![]() ;
;
(2)试判断![]() 与⊙O的位置关系,并说明理由;
与⊙O的位置关系,并说明理由;
(3)若![]() , 求
, 求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在9×7的小正方形网格中,△ABC的顶点A,B,C在网格的格点上.将△ABC向左平移3个单位、再向上平移3个单位得到△A′B′C′.再将△ABC按一定规律依次旋转:第1次,将△ABC绕点B顺时针旋转![]() 得到△
得到△![]() ;第2次,将△
;第2次,将△![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 得到△
得到△![]() ;第3次,将△
;第3次,将△![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 得到△
得到△![]() ;第4次,将△
;第4次,将△![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 得到△
得到△![]() 依次旋转下去.
依次旋转下去.

(1)在网格中画出△A′B′C′和△![]() ;
;
(2)请直接写出至少在第几次旋转后所得的三角形刚好为△A′B′C′.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=(x﹣1)2﹣4的图象先向左平移2个单位,再向上平移3个单位,所得函数解析式为( )
A.y=(x﹣1)2+1
B.y=(x﹣3)2﹣1
C.y=(x+1)2﹣1
D.y=(x+2)2+3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面推理正确的是( )
A. ∵a∥b,b∥c,∴c∥d B. ∵a∥c,b∥d,∴c∥d
C. ∵a∥b,a∥c,∴b∥c D. ∵a∥b,c∥d,∴a∥c
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1)是一个长为 ![]() ,宽为
,宽为 ![]() (
( ![]() >
> ![]() )的长方形,用剪刀沿图中虚线(对称轴)剪开,把它分成四块形状和大小都一样的小长方形,然后按图(2)那样拼成一个正方形,则中间空的部分的面积是.
)的长方形,用剪刀沿图中虚线(对称轴)剪开,把它分成四块形状和大小都一样的小长方形,然后按图(2)那样拼成一个正方形,则中间空的部分的面积是.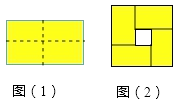
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com