
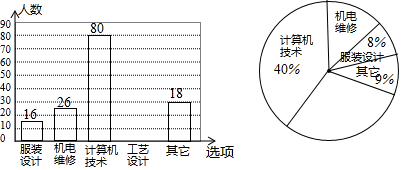
分析 (1)根据喜欢其它累的人数是18,所占的百分比是9%,据此即可求的调查的总人数,进而根据百分比的意义求得扇形统计图中每部分的百分比,补全统计图;
(2)利用总人数乘以对应的百分比即可;
(3)概率约等于对应的百分比即可作出解答.
解答 解(1)补全的扇形统计图和条形统计图如图所示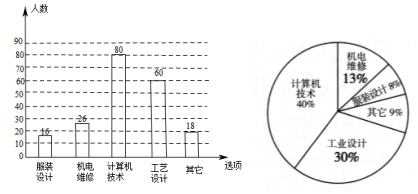
(2)3000×30%=900(人),
∴估计该校对“工业设计”最感兴趣的学生是900人;
(3)要从这些被调查的学生中随机抽取一人进行访谈,那么正好抽到对“机电维修”最感兴趣的学生的概率是 0.13(或13%或$\frac{13}{100}$).
点评 本题考查的是条形统计图的综合运用.读懂统计图,从统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
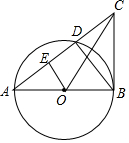 已知△ABC中,AB=8,BC=6,以AB为直径的⊙O与AC交于D点,连接BD,且BD=$\frac{24}{5}$.连接OC.
已知△ABC中,AB=8,BC=6,以AB为直径的⊙O与AC交于D点,连接BD,且BD=$\frac{24}{5}$.连接OC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
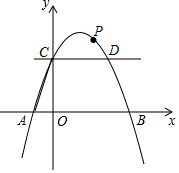 如图,在平面直角坐标系中,抛物线y=-$\frac{1}{2}$x2+bx+c与x轴交于A、B两点,点A、B的坐标分别是(-1,0)、(5,0),与y轴交于点C,连接AC,过点C作CD∥x轴交抛物线于点D,点P是抛物线上一个动点,设点P的横坐标为m.
如图,在平面直角坐标系中,抛物线y=-$\frac{1}{2}$x2+bx+c与x轴交于A、B两点,点A、B的坐标分别是(-1,0)、(5,0),与y轴交于点C,连接AC,过点C作CD∥x轴交抛物线于点D,点P是抛物线上一个动点,设点P的横坐标为m.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
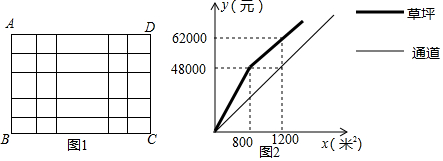
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -3<m<-2 | B. | -3≤m<-2 | C. | -3≤m≤-2 | D. | -3<m≤-2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
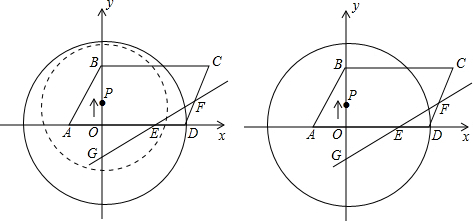
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
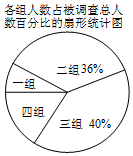 “读书”是一种诗意的生存状态,一种幸福的生活方式,一种温暖的生命体验.随着央视《朗读者》的播出,某校带领全体师生走进阅读,洗涤心灵.某班同学为了解该校学生每周课外阅读的时间,在全校随机调查了部分学生,对这部分同学的课外阅读时间x(小时)进行了整理,并制作了如下不完全的统计表格和扇形统计图:
“读书”是一种诗意的生存状态,一种幸福的生活方式,一种温暖的生命体验.随着央视《朗读者》的播出,某校带领全体师生走进阅读,洗涤心灵.某班同学为了解该校学生每周课外阅读的时间,在全校随机调查了部分学生,对这部分同学的课外阅读时间x(小时)进行了整理,并制作了如下不完全的统计表格和扇形统计图:| 组号 | 分组 | 频数 |
| 一 | 0≤x<2 | 4 |
| 二 | 2≤x<4 | 18 |
| 三 | 4≤x<6 | a |
| 四 | 6≤x<8 | 8 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com