
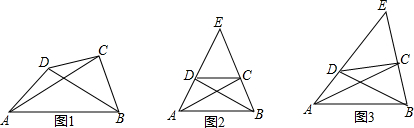
分析 (1)根据等边对等角可得∠EAB=∠EBA,根据四边形ABCD是互补等对边四边形,可得AD=BC,根据SAS可证△ABD≌△BAC,根据全等三角形的性质可得∠ABD=∠BAC,再根据等腰三角形的性质即可证明;
(2)仍然成立;理由如下:如图所示:过点A、B分别作BD的延长线与AC的垂线,垂足分别为G、F,证明△AGD≌△BFC,得到AG=BF,又AB=BA,所以△ABC≌△BAF,得到∠ABD=∠BAC,根据∠ADB+∠BCA=180°,得到∠EDB+∠ECA=180°,进而得到∠AEB+∠DHC=180°,由∠DHC+∠BHC=180°,所以∠AEB=∠BHC.因为∠BHC=∠BAC+∠ABD,∠ABD=∠BAC,所以∠ABD=∠BAC=$\frac{1}{2}$∠AEB.
解答 解:(1)∵AE=BE,
∴∠EAB=∠EBA,
∵四边形ABCD是互补等对边四边形,
∴AD=BC,
在△ABD和△BAC中,
$\left\{\begin{array}{l}{AD=BC}&{\;}\\{∠DAB=∠CBA}&{\;}\\{AB=BA}&{\;}\end{array}\right.$,
∴△ABD≌△BAC(SAS),
∴∠ADB=∠BCA,
又∵∠ADB+∠BCA=180°,
∴∠ADB=∠BCA=90°,
在△ABE中,∵∠EAB=∠EBA=$\frac{180°-∠AEB}{2}$=90°-$\frac{1}{2}$∠AEB,
∴∠ABD=90°-∠EAB=90°-(90°-$\frac{1}{2}$∠AEB)=$\frac{1}{2}$∠AEB,
同理:∠BAC=$\frac{1}{2}$∠AEB,
∴∠ABD=∠BAC=$\frac{1}{2}$∠AEB;
(2)仍然成立;
理由如下:如图③所示:过点A、B分别作BD的延长线与AC的垂线,垂足分别为G、F,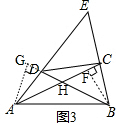
∵四边形ABCD是互补等对边四边形,
∴AD=BC,∠ADB+∠BCA=180°,
又∠ADB+ADG=180°,
∴∠BCA=∠ADC,
又∵AG⊥BD,BF⊥AC,
∴∠AGD=∠BFC=90°,
在△AGD和△BFC中,
$\left\{\begin{array}{l}{∠AGD=∠BFC}\\{∠BCA=∠ADC}\\{AD=BC}\end{array}\right.$
∴△AGD≌△BFC,
∴AG=BF,
在△ABG和△BAF中,
$\left\{\begin{array}{l}{AB=BA}\\{AG=BF}\end{array}\right.$
∴△ABG≌△BAF,
∴∠ABD=∠BAC,
∵∠ADB+∠BCA=180°,
∴∠EDB+∠ECA=180°,
∴∠AEB+∠DHC=180°,
∵∠DHC+∠BHC=180°,
∴∠AEB=∠BHC.
∵∠BHC=∠BAC+∠ABD,∠ABD=∠BAC,
∴∠ABD=∠BAC=$\frac{1}{2}$∠AEB.
点评 本题考查了等腰三角形的性质、全等三角形的判定与性质,解决本题的关键是根据SAS证明△ABD≌△BAC.


 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{24}$ | B. | $\sqrt{36}$ | C. | $\sqrt{\frac{a}{b}}$ | D. | $\sqrt{a+4}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
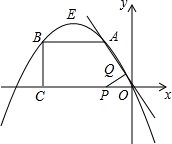 已知:如图,在四边形OABC中,AB∥OC,BC⊥x轴于点C、A(-1,1),B(-3,1)动点P从点O出发,沿着x轴负方向以每秒2个单位长度的速度移动,过点P作PQ垂直与直线OA,垂足为点Q,设点P移动的时间t秒(0<t<2)
已知:如图,在四边形OABC中,AB∥OC,BC⊥x轴于点C、A(-1,1),B(-3,1)动点P从点O出发,沿着x轴负方向以每秒2个单位长度的速度移动,过点P作PQ垂直与直线OA,垂足为点Q,设点P移动的时间t秒(0<t<2)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
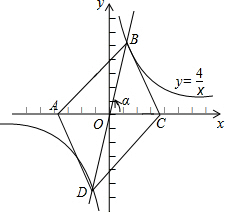 如图,在同一直角坐标系中,正比例函数的图象可以看作是:将x轴所在的直线绕原点O逆时针旋转α度(0<α<90)后的图形,若它与反比例函数y=$\frac{4}{x}$的图象分别交一、三象限的点B、D,已知点A(-m,0)、C(m,0)(m>0)
如图,在同一直角坐标系中,正比例函数的图象可以看作是:将x轴所在的直线绕原点O逆时针旋转α度(0<α<90)后的图形,若它与反比例函数y=$\frac{4}{x}$的图象分别交一、三象限的点B、D,已知点A(-m,0)、C(m,0)(m>0)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
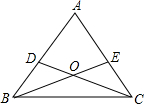 如图,已知△ABC中,AB=AC,点D、E分别在AB、AC上,且BD=CE.
如图,已知△ABC中,AB=AC,点D、E分别在AB、AC上,且BD=CE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某校开展第二课堂活动,准备组建舞蹈、武术、球类(足球、篮球、乒乓球、羽毛球)、花样滑冰四类社团、为了解在校学生对这4个社团活动的喜爱情况,学校随机抽取部分学生进行了“你最喜爱的社团”调查,依据相关数据绘制成以下不完整的统计表,请根据图表中的信息解答下列问题:
某校开展第二课堂活动,准备组建舞蹈、武术、球类(足球、篮球、乒乓球、羽毛球)、花样滑冰四类社团、为了解在校学生对这4个社团活动的喜爱情况,学校随机抽取部分学生进行了“你最喜爱的社团”调查,依据相关数据绘制成以下不完整的统计表,请根据图表中的信息解答下列问题:| 社团类别 | 人数 | 占总人数的比例 |
| 舞蹈 | b | 25% |
| 武术 | 24 | 10% |
| 花样滑冰 | 36 | n% |
| 球类 | a | 50% |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 5×10-6 | B. | 25×10-5 | C. | 2.5×10-4 | D. | 2.5×10-5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com