
分析 (1)可设购买1副乒乓球拍需x元、1副羽毛球拍需y元,根据等量关系:①购买2副乒乓球拍和1副羽毛球拍共需540元,②购买1副乒乓球拍和2副羽毛球拍共需660元,列出方程组求解即可;
(2)可设该单位购买k副羽毛球拍,则乒乓球拍为(10-k)副,根据购买乒乓球拍、羽毛球拍的总费用不超过2500元,列出不等式求解即可.
解答 解:(1)设购买1副乒乓球拍需x元、1副羽毛球拍需y元,依题意有
$\left\{\begin{array}{l}{2x+y=540}\\{x+2y=660}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=140}\\{y=260}\end{array}\right.$.
答:购买1副乒乓球拍需140元、1副羽毛球拍需260元;
(2)设该单位购买k副羽毛球拍,则乒乓球拍为(10-k)副,依题意有
260k+140(10-k)≤2500,
解得k≤$\frac{55}{6}$,
∵k为整数,
∴k最多为9.
故该单位最多可以购买9副羽毛球拍.
点评 考查了二元一次方程组的应用,一元一次不等式的应用,解决问题的关键是读懂题意,找到关键描述语,找到所求的量的等量关系和不等量关系.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源: 题型:填空题
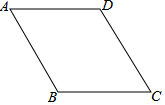 如图,在菱形ABCD中,∠ABC=120°,AB=10cm,点P是这个菱形内部或边上的一点.若以P,B,C为顶点的三角形是等腰三角形,则P,A(P,A两点不重合)两点间的最短距离为10$\sqrt{3}$-10cm.
如图,在菱形ABCD中,∠ABC=120°,AB=10cm,点P是这个菱形内部或边上的一点.若以P,B,C为顶点的三角形是等腰三角形,则P,A(P,A两点不重合)两点间的最短距离为10$\sqrt{3}$-10cm.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
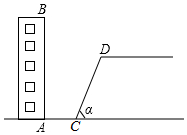 如图,某校教学楼AB后方有一斜坡,已知斜坡CD的长为12米,坡角α为60°,根据有关部门的规定,∠α≤39°时,才能避免滑坡危险,学校为了消除安全隐患,决定对斜坡CD进行改造,在保持坡脚C不动的情况下,学校至少要把坡顶D向后水平移动多少米才能保证教学楼的安全?(结果取整数)
如图,某校教学楼AB后方有一斜坡,已知斜坡CD的长为12米,坡角α为60°,根据有关部门的规定,∠α≤39°时,才能避免滑坡危险,学校为了消除安全隐患,决定对斜坡CD进行改造,在保持坡脚C不动的情况下,学校至少要把坡顶D向后水平移动多少米才能保证教学楼的安全?(结果取整数)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 73 | B. | 74 | C. | 75 | D. | 76 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| A户型 | B户型 | |
| 套数 | x | 80-x |
| 利润(万元) | 12x | 10(80-x) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
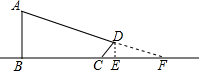 小明在某一时刻测得1m的杆子在阳光下的影子长为2m,他想测量电线杆AB的高度,但其影子恰好落在土坡的坡面CD和地面BC上,量得CD=4m,BC=10m,CD与底面成45°,求电线杆的高度.
小明在某一时刻测得1m的杆子在阳光下的影子长为2m,他想测量电线杆AB的高度,但其影子恰好落在土坡的坡面CD和地面BC上,量得CD=4m,BC=10m,CD与底面成45°,求电线杆的高度.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
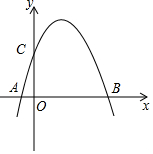 如图,已知抛物线y=ax2+bx+c(a≠0)经过A(-1,0),B(3,0),C(0,3)三点,O为坐标原点.
如图,已知抛物线y=ax2+bx+c(a≠0)经过A(-1,0),B(3,0),C(0,3)三点,O为坐标原点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com