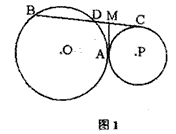
阅读下面一段文字,完成后面的问题.如图1,⊙O与⊙P外切于点A,BC切⊙P于C,交⊙O于B、D,AM是内公切线,交BC于M,若D是BC的中点,设BD=a,DM=b,探索此时a与b之间的关系.以下是某同学解答过程中的一部分:
解:∵MA、MC分别切⊙O于A、C,
∴MA=MC,
∴MC
2=MA
2=MD·MB=b·(b+a),
∴MC=
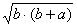
.
又∵D是BC的中点,即DB=DC=DM+MC,
∴a=b+
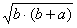
,变形得:a-b=
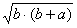
,
两边平方得:___________ .
∴整理得a与b所满足的关系为 ____________.
问题:(1)补全以上解答过程(填在上文横线上):
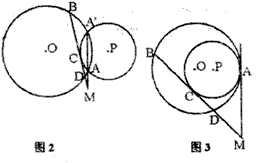
(2)若⊙O不动,把⊙P向左平移,分别得图2,图3,而AM变为割线或外公切线,将题中的条件改为:“D为CM的中点,设BD=a,DM=b”,此时a与b满足的关系式是 __________.请证明你从图2或图3中得到的结论(只选用一个图形证明即可).

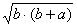 .
.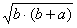 ,变形得:a-b=
,变形得:a-b=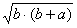 ,
,