
(1)操作发现
如图,矩形ABCD中,E是AD的中点,将△ABE沿BE折叠后得到△GBE,且点G在举行ABCD内部.小明将BG延长交DC于点F,认为GF=DF,你同意吗?说明理由.

(2)问题解决
保持(1)中的条件不变,若DC=2DF,求![]() 的值;
的值;
(3)类比探求
保持(1)中条件不变,若DC=nDF,求![]() 的值.
的值.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:


查看答案和解析>>
科目:初中数学 来源: 题型:
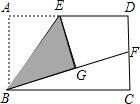 (2011•曲阜市模拟)(1)操作发现
(2011•曲阜市模拟)(1)操作发现| AD | AB |
查看答案和解析>>
科目:初中数学 来源: 题型:
 全等除外),并给出证明过程;
全等除外),并给出证明过程;| AD |
| AB |
| AD |
| AB |
查看答案和解析>>
科目:初中数学 来源: 题型:
(1)操作发现
如图,矩形ABCD中,E是AD的中点,将△ABE沿BE折叠后得到△GBE,且点G在矩行ABCD内部.小明将BG延长交DC于点F,认为GF=DF,你同意吗?说明理由.
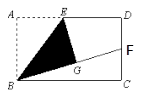
(2)问题解决保持(1)中的条件不变,若DC=2DF,求![]() 的值;
的值;
(3)类比探求保持(1)中条件不变,若DC=nDF,求![]() 的值
的值
查看答案和解析>>
科目:初中数学 来源: 题型:

 的值;
的值; 的值
的值查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com