




 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
 如图所示,在Rt△ABC中,∠C=90°,∠B=40°,BC=10,解这个直角三角形(精确到0.1)(sin40°≈0.643,cos40°≈0.766,tan40°≈0.839)
如图所示,在Rt△ABC中,∠C=90°,∠B=40°,BC=10,解这个直角三角形(精确到0.1)(sin40°≈0.643,cos40°≈0.766,tan40°≈0.839)查看答案和解析>>
科目:初中数学 来源: 题型:
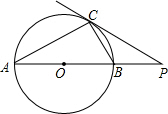 如图,AB是⊙O的直径,点P是AB延长线上一点,PC切⊙O于点C,连AC.
如图,AB是⊙O的直径,点P是AB延长线上一点,PC切⊙O于点C,连AC.| 3 |
| 5 |
| 13 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 世界杯比赛中,根据场上攻守形势,守门员会在门前来回跑动,如果以球门线为基准,向前跑记作正数,返回则记作负数,一段时间内,某守门员的跑动情况记录如下(单位:m):+10,-2,+5,-6,+12,-9,+4,-14.(假定开始计时时,守门员正好在球门线上)
世界杯比赛中,根据场上攻守形势,守门员会在门前来回跑动,如果以球门线为基准,向前跑记作正数,返回则记作负数,一段时间内,某守门员的跑动情况记录如下(单位:m):+10,-2,+5,-6,+12,-9,+4,-14.(假定开始计时时,守门员正好在球门线上)查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,小敏同学想测量一棵大树的高度.她站在B处仰望树顶,测得仰角为30°,再往大树的方向前进4m到点C,测得仰角为60°,已知小敏同学身高(AB)为1.6m,求这棵树的高度(DF).(结果精确到0.1m,
如图,小敏同学想测量一棵大树的高度.她站在B处仰望树顶,测得仰角为30°,再往大树的方向前进4m到点C,测得仰角为60°,已知小敏同学身高(AB)为1.6m,求这棵树的高度(DF).(结果精确到0.1m,| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| A、3 | B、9 | C、7 | D、1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com