
 在平面直角坐标系中给定以下五个点A(-3,0),B(-1,4),C(0,3),D(
在平面直角坐标系中给定以下五个点A(-3,0),B(-1,4),C(0,3),D(| 1 |
| 2 |
| 7 |
| 4 |
| 15 |
| 4 |
| 17 |
| 4 |
| 17 |
| 4 |
| 17 |
| 4 |
| 1 |
| 2 |
| 7 |
| 4 |
| 17 |
| 4 |
| 17 |
| 4 |
| 17 |
| 4 |
| 17 |
| 4 |
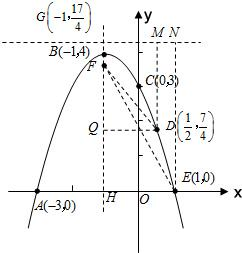 解:(1)设抛物线的解析式为y=ax2+bx+c,
解:(1)设抛物线的解析式为y=ax2+bx+c,
|
| 17 |
| 4 |
| 17 |
| 4 |
| 15 |
| 4 |
| HE2+HF2 |
| 17 |
| 4 |
| 17 |
| 4 |
| 17 |
| 4 |
| 17 |
| 4 |
| 7 |
| 4 |
| 10 |
| 4 |
| 5 |
| 2 |
| 3 |
| 2 |
| 15 |
| 4 |
| 7 |
| 4 |
| 8 |
| 4 |
| QF2+QD2 |
| 5 |
| 2 |
| 17 |
| 4 |
| 17 |
| 4 |


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:初中数学 来源: 题型:
| ||||
| a+2 |
| k |
| 2 |
| k |
| 2 |
| PM+PN |
| NM |
| PM-PN |
| AM |

查看答案和解析>>
科目:初中数学 来源: 题型:
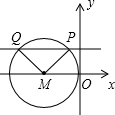 如图,在平面直角坐标系中,⊙M与y轴相切于原点O,平行于x轴的直线交⊙M于P,Q两点,点P在点Q的右方,若点P的坐标是(-1,2),有下列结论:①点Q的坐标是(-4,2);②PQ=3;③△MPQ的面积是3;④M点的坐标是(-3,0).其中正确的结论序号是
如图,在平面直角坐标系中,⊙M与y轴相切于原点O,平行于x轴的直线交⊙M于P,Q两点,点P在点Q的右方,若点P的坐标是(-1,2),有下列结论:①点Q的坐标是(-4,2);②PQ=3;③△MPQ的面积是3;④M点的坐标是(-3,0).其中正确的结论序号是查看答案和解析>>
科目:初中数学 来源: 题型:
 (2013•安庆二模)在平面直角坐标系中.过一点分別作x轴与y轴的垂线,若与坐标轴围成矩形的周长与面积相等,则这个点叫做和谐点.给出以下结论:①点M(2,4)是和谐点;②不论a为何值时,点P(2,a)不是和谐点;③若点P(a,3)是和谐点,则a=6;④若点F是和谐点,则点F关于坐标轴的对称点也是和谐点.正确结论的序号是
(2013•安庆二模)在平面直角坐标系中.过一点分別作x轴与y轴的垂线,若与坐标轴围成矩形的周长与面积相等,则这个点叫做和谐点.给出以下结论:①点M(2,4)是和谐点;②不论a为何值时,点P(2,a)不是和谐点;③若点P(a,3)是和谐点,则a=6;④若点F是和谐点,则点F关于坐标轴的对称点也是和谐点.正确结论的序号是查看答案和解析>>
科目:初中数学 来源: 题型:
 (2012•老河口市模拟)如图,在平面直角坐标系中,抛物线y=ax2+bx+c交y轴于A(0,4),交x轴于B、C两点(点B在点C的左侧).B、C两点坐标分别为(3,0),(8,0).
(2012•老河口市模拟)如图,在平面直角坐标系中,抛物线y=ax2+bx+c交y轴于A(0,4),交x轴于B、C两点(点B在点C的左侧).B、C两点坐标分别为(3,0),(8,0).查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com