
分析 (1)设步行速度为x米/分,则自行车的速度为2.5x米/分,根据等量关系:骑自行车到学校比他从学校步行到家用时少20分钟可得出方程,解出即可;
(2)计算出步行、骑车及在家拿作业的时间和,然后与37比较即可作出判断.
解答 解:(1)设步行速度为x米/分,则自行车的速度为2.5x米/分,
根据题意得:$\frac{1500}{x}$=$\frac{1500}{2.5x}$+15,
解得:x=60,
经检验x=60是原方程的解.
答:李强步行的速度是60米/分.
(2)根据题意得,李强总共需要:$\frac{1500}{60}$+$\frac{1500}{2.5×60}$+1=36<37.
即李强能上课之前赶到学校.
答:能在上课开始前赶到学校.
点评 此题考查了分式方程的应用,设出步行的速度,根据等量关系得出方程是解答本题的关键,注意分式方程一定要检验.


 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
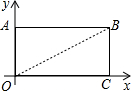 在平面直角坐标系中,点A(x,y),点A′(x′,y′),若x′=x+m,y′=y+n,即点A′(x+m,y+n),则表示点A到点A′的一个平移.例如:点A(x,y),点A′(x′,y′),若x′=x+1,y′=y-2,则表示A向右平移1个单位,再向下平移2个单位得到点A′.
在平面直角坐标系中,点A(x,y),点A′(x′,y′),若x′=x+m,y′=y+n,即点A′(x+m,y+n),则表示点A到点A′的一个平移.例如:点A(x,y),点A′(x′,y′),若x′=x+1,y′=y-2,则表示A向右平移1个单位,再向下平移2个单位得到点A′.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
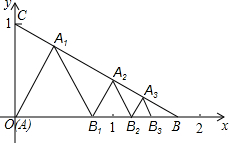 如图所示,已知在△ABC中,A(0,0),B($\sqrt{3}$,0),C(0,1),在△ABC内依次作等边三角形,作出的等边三角形分别是第1个△AA1B1,第2个△B1A2B2,第3个△B2A3B3,…,使B1、B2、B3、…在x轴上,A1、A2、A3、…在BC边上,则第n个等边三角形的边长等于( )
如图所示,已知在△ABC中,A(0,0),B($\sqrt{3}$,0),C(0,1),在△ABC内依次作等边三角形,作出的等边三角形分别是第1个△AA1B1,第2个△B1A2B2,第3个△B2A3B3,…,使B1、B2、B3、…在x轴上,A1、A2、A3、…在BC边上,则第n个等边三角形的边长等于( )| A. | $\frac{\sqrt{3}}{{2}^{n}}$ | B. | $\frac{\sqrt{3}}{{2}^{n-1}}$ | C. | $\frac{3}{{2}^{n}}$ | D. | $\frac{3}{{2}^{n-1}}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com