练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
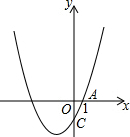
    5．如图，抛物线y=x2+2x-3与x轴正半轴，y轴分别交于点A、C，若点P在抛物线上，且△POC的面积是△AOC的面积的4倍，求点P的坐标．

    分析 首先求得A的坐标，△POC的面积是△AOC的面积的4倍，据此即可求得P的横坐标，代入函数解析式即可求得P的坐标．

    解答 解：令y=x2+2x-3中令y=0，则x2+2x-3=0，
    解得：x1=-3，x2=1，
    则A的坐标是（1，0）．
    ∵△POC的面积是△AOC的面积的4倍，
    ∴P的横坐标是4或-4．
    当x=-4时，y=16-8-3=5，则P的坐标是（-4，5）；
    当x=4时，y=16+8-3=21，则P的坐标是（4，21）．
    故P的坐标是（-4，5）或（4，21）．

    点评 本题考查了二次函数与坐标轴的交点，正确根据△POC的面积是△AOC的面积的4倍，利用A的横坐标求得P的横纵标是关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    19．观察下面一列数，探究其中的规律：
    -1，$\frac{1}{2}$，-$\frac{1}{3}$，$\frac{1}{4}$，$-\frac{1}{5}$，$\frac{1}{6}$
    （1）填空：第11，12，13三个数分别是-$\frac{1}{11}$，$\frac{1}{12}$，-$\frac{1}{13}$；
    （2）第2015个数是什么？第2016个呢？
    （3）如果这列数无限排列下去，与哪个数越来越近？

    查看答案和解析>>

    科目：初中数学 来源：2016-2017学年吉林省七年级下学期期中数学模拟试卷（四）（解析版） 题型：单选题

    下列方程是二元一次方程的是( )

    A. 2x+y=z-3 B. xy=5 C. 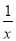+5=3y D. x=y

    查看答案和解析>>

    科目：初中数学 来源：2017届山东省中考模拟数学试卷（解析版） 题型：单选题

    在平面直角坐标系中，直线y=﹣x+2与反比例函数y=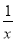的图象有唯一公共点，若直线y=﹣x+b与反比例函数y=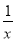的图象有2个公共点，则b的取值范围是（　　）

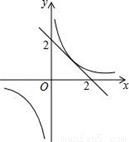
    A. b＞2 B. ﹣2＜b＜2 C. b＞2或b＜﹣2 D. b＜﹣2

    查看答案和解析>>

    科目：初中数学 来源：2017届山东省中考模拟数学试卷（解析版） 题型：单选题

    下列计算正确的是（　　）

    A. a3+a2=a5 B. a3﹣a2=a C. a3•a2=a6 D. a3÷a2=a

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    10．在平面直角坐标系中，如果横坐标与纵坐标都是整数的点称为整点，将二次函数y=x2+6x-$\frac{27}{4}$的图象与x轴所围成的封闭图形染成红色，则在此红色区域内部及其边界上的整点的个数是（　　）
    A．8B．7C．6D．5

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    17．已知抛物线y=-x2-（m-4）x+3（m-1）与x轴交于A，B两点，与y轴交于C点．
    （1）求m的取值范围；
    （2）若m＜0，直线y=kx-1经过点A并与y轴交于点D，且AD•BD=5$\sqrt{2}$，求抛物线的解析式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

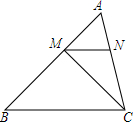    14．如图，△ABC中，BC=4，∠B=45°，AB=3$\sqrt{2}$，M、N分别是AB、AC上的点，MN∥BC．设MN=x，△MNC的面积为S．
    （1）求出S与x之间的函数关系式，并写出自变量x的取值范围；
    （2）是否存在平行于BC的线段MN，使△MNC的面积等于2？若存在，请求出MN的长；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    15．（1）如图①，D是等边三角形ABC的AB边上一个动点（点D与点A，B不重合），连接DC，以DC为边在BC上方作等边三角形DCE，连接AE，求证：∠B=∠EAC；
    （2）如图②，当动点D运动至等边三角形ABC边BA的延长线上时，其他作法与（1）相同，（1）中结论∠B=∠EAC还成立吗？请说明理由；
    （3）如图③，在等腰三角形ABC中，AB=AC，D是AB上任意一点（点D与A，B不重合），连结CD，以CD为底边作等腰三角形ECD，使顶角∠DEC=∠BAC，连结AE，试探究∠B与∠EAC的数量关系，并说明理由．

    查看答案和解析>>

    同步练习册答案