
【题目】如图,每小正方形的边长为![]() 个单位,每个小方格的顶点叫格点.
个单位,每个小方格的顶点叫格点.

(1)画出![]() 的
的![]() 边上的中线
边上的中线![]() ;
;
(2)画出![]() 向右平移
向右平移![]() 个单位后得到的
个单位后得到的![]() ;
;
(3)图中![]() 与
与![]() 的关系是 ;
的关系是 ;
(4)能使![]() 的格点
的格点![]() (不同于点
(不同于点![]() ),共有 个,在图中分别用
),共有 个,在图中分别用![]() 、
、![]() 、
、![]() 表示出来.
表示出来.
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a≠0)与x轴交于A(﹣4,0),B(2,0),与y轴交于点C(0,2). 
(1)求抛物线的解析式;
(2)若点D为该抛物线上的一个动点,且在直线AC上方,当以A,C,D为顶点的三角形面积最大时,求点D的坐标及此时三角形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
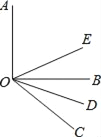
【题目】如图所示,OE,OD分别平分∠AOC和∠BOC,
(1)如果∠AOB=90°,∠BOC=38°,求∠DOE的度数;
(2)如果∠AOB=α,∠BOC=β(α、β均为锐角,α>β),其他条件不变,求∠DOE;
(3)从(1)、(2)的结果中,你发现了什么规律,请写出来.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学九年级学生开展测量物体高度的实践活动,他们要测量学校一幢教学楼的高度,如图,他们先在点C测得教学楼AB的顶点A的仰角为30°,然后向教学楼前进20米到达点D,又测得点A的仰角为45°,请根据这些数据,求这幢教学楼的高度.(最后结果精确到1米,参考数据 ![]() ≈1.732)
≈1.732) 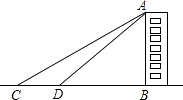
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,AD、BE、CF分别是三边上的中线.
(1)若AC=1,BC=![]() .求证:AD2+CF2=BE2;
.求证:AD2+CF2=BE2;
(2)是否存在这样的Rt△ABC,使得它三边上的中线AD、BE、CF的长恰好是一组勾股数?请说明理由.(提示:满足关系a2+b2=c2的3个正整数a、b、c称为勾股数.)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司拟为贫困山区建一所希望小学,甲、乙两个工程队提交了投标方案,若独立完成该项目,则甲工程队所用时间是乙工程队的1.5倍;若甲、乙两队合作完成该项目,则共需72天.
(1)甲、乙两队单独完成建校工程各需多少天?
(2)若由甲工程队单独施工,平均每天的费用为0.8万元,为了缩短工期,该公司选择了乙工程队,但要求其施工的总费用不能超过甲工程队,求乙工程队平均每天的施工费用最多为多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD∥BC,AF平分∠BAD交BC于点F,BE平分∠ABC交AD于点E.求证: 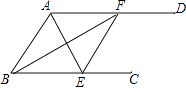
(1)△ABF是等腰三角形;
(2)四边形ABFE是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,抛物线y=ax2+bx+3(a≠0)与x轴、y轴分别交于点A(﹣1,0)、B(3,0)、点C三点.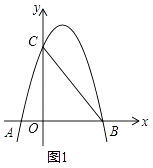
(1)试求抛物线的解析式;
(2)点D(2,m)在第一象限的抛物线上,连接BC,BD.试问,在对称轴左侧的抛物线上是否存在一点P,满足∠PBC=∠DBC?如果存在,请求出点P点的坐标;如果不存在,请说明理由;
(3)如图2,在(2)的条件下,将△BOC沿x轴正方向以每秒1个单位长度的速度向右平移,记平移后的三角形为△B′O′C′.在平移过程中,△B′O′C′与△BCD重叠的面积记为S,设平移的时间为t秒,试求S与t之间的函数关系式?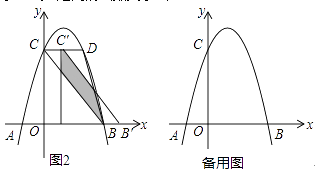
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com