解:(Ⅰ)∵抛物线与x轴的负半轴交于点A,与y轴的正半轴交于点B,若c=2,
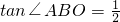
,
∴tan∠ABO=
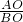
=

,
∴A(-1,0),
代入解析式y
2=x
2+ax+c,
∴0=1-a+2,
∴a=3,
∴y
2=x
2+3x+2;
(Ⅱ)∵c>0,
∴y
2-y
1=x
2+ax+c-[(a+1)x-1],
=(x-

)
2+

+c,
y
2-y
1>0,
∴在实数范围内,对于x的同一个值,直线与抛物线对应的y
1<y
2均成立;
(Ⅲ)当a=-1时,抛物线为y
2=x
2-x+c,且与x轴有公共点.
对于方程x
2-x+c=0,判别式△=1-4c≥0,有c≤

.
①当 c=

时,由方程x
2-x+

=0,解得x
1=x
2=

.
此时抛物线与x轴只有一个公共点(

,0);
②当 c<

时,x
1=-1时,y
1=2+c;
x
2=4时,y
2=12+c.
由已知-1<x<4时,该抛物线与x轴有公共点,考虑其对称轴为 x=

,
应有 即

解得-12<c≤-2.
综上,c=

或-12<c≤-2.
分析:(Ⅰ)根据tan∠ABO=
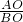
=

的值代入可得抛物线的解析式;
(Ⅱ)根据y
2-y
1=x
2+ax+c-[(a+1)x-1],直接化简配方即可得出答案;
(Ⅲ)把a代入解析式可得△=1-4c≥0,等于0时可直接求得c的值;求出y的相应的值后可得c的取值范围.
点评:此题主要考查了二次函数的综合应用以及图象与坐标轴有交点的条件,根据不等式的性质以及判别式得出c的取值范围是解决问题的关键.

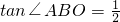 ,求抛物线的解析式;
,求抛物线的解析式;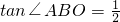 ,
,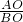 =
= ,
, )2+
)2+ +c,
+c, .
. 时,由方程x2-x+
时,由方程x2-x+ =0,解得x1=x2=
=0,解得x1=x2= .
. ,0);
,0); 时,x1=-1时,y1=2+c;
时,x1=-1时,y1=2+c; ,
,
 或-12<c≤-2.
或-12<c≤-2.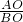 =
= 的值代入可得抛物线的解析式;
的值代入可得抛物线的解析式;

 问栏杆多少长时,所用拉力F最小?是多少?
问栏杆多少长时,所用拉力F最小?是多少?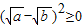 ,所以
,所以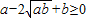 ,所以
,所以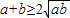 ,只有当a=b时,等号成立.
,只有当a=b时,等号成立.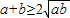 (a,b均为正实数)中,若ab为定值p,则
(a,b均为正实数)中,若ab为定值p,则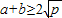 ,只有当a=b时,a+b有最小值
,只有当a=b时,a+b有最小值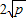 .
.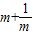 有最小值______;
有最小值______;