
【题目】如图,已知抛物线l1:y=![]() (x﹣2)2﹣2与x轴分别交于O、A两点,将抛物线l1向上平移得到l2 , 过点A作AB⊥x轴交抛物线l2于点B,如果由抛物线l1、l2、直线AB及y轴所围成的阴影部分的面积为16,则抛物线l2的函数表达式为( )
(x﹣2)2﹣2与x轴分别交于O、A两点,将抛物线l1向上平移得到l2 , 过点A作AB⊥x轴交抛物线l2于点B,如果由抛物线l1、l2、直线AB及y轴所围成的阴影部分的面积为16,则抛物线l2的函数表达式为( )
A.y=![]() (x﹣2)2+4
(x﹣2)2+4
B.y=![]() (x﹣2)2+3
(x﹣2)2+3
C.y=![]() (x﹣2)2+2
(x﹣2)2+2
D.y=![]() (x﹣2)2+1
(x﹣2)2+1
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,对角线AC、BD交于点O,以OB为直径画圆M,过D作⊙M的切线,切点为N,分别交AC、BC于点E、F,已知AE=5,CE=3,则DF的长是( )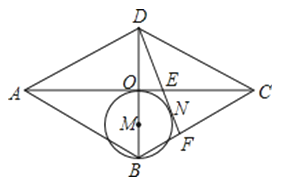
A.3
B.4
C.4.8
D.5
查看答案和解析>>
科目:初中数学 来源: 题型:
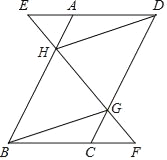
【题目】已知:如图,在ABCD中,延长DA到点E,延长BC到点F,使得AE=CF,连接EF,分别交AB,CD于点H,G,连接DH,BG.
(1)求证:△AEH≌△CFG;
(2)连接BE,若BE=DE,则四边形BGDH是什么特殊四边形?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现代互联网技术的广泛应用,催生了快递行业的告诉发展,小明计划给朋友快递一部分物品,经了解有甲乙两家快递公司比较合适.甲公司表示:快递物品不超过![]() 千克的,按每千克
千克的,按每千克![]() 元收费;超过
元收费;超过![]() 千克,超过的部分按每千克
千克,超过的部分按每千克![]() 元收费.设小明快递物品
元收费.设小明快递物品![]() 千克.
千克.
![]() 用含有
用含有![]() 的代数式表示小明快递物品的费用;
的代数式表示小明快递物品的费用;
![]() 若小明快递物品
若小明快递物品![]() 千克,应付快递费多少元?
千克,应付快递费多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在梯形ABCD中,AD∥BC,∠B=90°,AD=24cm,BC=26cm,动点P从点A出发沿AD方向向点D以1cm/s的速度运动,动点Q从点C开始沿着CB方向向点B以3cm/s的速度运动.点P、Q分别从点A和点C同时出发,当其中一点到达端点时,另一点随之停止运动.
(1)经过多长时间,四边形PQCD是平行四边形?
(2)经过多长时间,四边形PQBA是矩形?
(3)经过多长时间,当PQ不平行于CD时,有PQ=CD.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数y=kx-5的图象经过点A(2,-1).
(1)求k的值;
(2)画出这个函数的图象;
(3)若将此函数的图象向上平移m个单位后与坐标轴围成的三角形的面积为1,请直接写出m的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个能被13整除的自然数我们称为“十三数”,“十三数”的特征是:若把这个自然数的末三位与末三位以前的数字组成的数之差,如果能被13整除,那么这个自然数就一定能被13整除.例如:判断383357能不能被13整除,这个数的末三位数字是357,末三位以前的数字组成的数是383,这两个数的差是383﹣357=26,26能被13整除,因此383357是“十三数”.
(1)判断3253和254514是否为“十三数”,请说明理由.
(2)若一个四位自然数,千位数字和十位数字相同,百位数字与个位数字相同,则称这个四位数为“间同数”.
①求证:任意一个四位“间同数”能被101整除.
②若一个四位自然数既是“十三数”,又是“间同数”,求满足条件的所有四位数的最大值与最小值之差.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com