
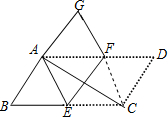
 将?ABCD纸片沿EF折叠,使点C与点A重合,点D落在点G处.
将?ABCD纸片沿EF折叠,使点C与点A重合,点D落在点G处. ,AC•EF=y,试求y与x之间的函数关系式.
,AC•EF=y,试求y与x之间的函数关系式. 解:(1)∵四边形ABCD是平行四边形,
解:(1)∵四边形ABCD是平行四边形,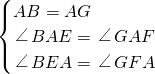
 ,
, =x=
=x= ,
, ,得出△AEC的面积等于4x,进而得出菱形AECF的面积等于8x,得出答案即可.
,得出△AEC的面积等于4x,进而得出菱形AECF的面积等于8x,得出答案即可. ,得出
,得出 =x,进而得出△AEC的面积等于4x是解题关键.
=x,进而得出△AEC的面积等于4x是解题关键. 

科目:初中数学 来源: 题型:
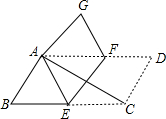 将?ABCD纸片沿EF折叠,使点C与点A重合,点D落在点G处(如图).
将?ABCD纸片沿EF折叠,使点C与点A重合,点D落在点G处(如图).| EC | BC |
查看答案和解析>>
科目:初中数学 来源: 题型:
 (2012•周口二模)将?ABCD纸片沿EF折叠,使点C与点A重合,点D落在点G处.
(2012•周口二模)将?ABCD纸片沿EF折叠,使点C与点A重合,点D落在点G处.| EC | BC |
查看答案和解析>>
科目:初中数学 来源: 题型:
将□ABCD纸片沿EF折叠,使点C与点A重合,点D落在点G处.
1.求证:△ABE≌△AGF.
2.连结AC,若□ABCD的面积等于8,![]() ,
,![]() ,试求y与x之间的函数关系式.
,试求y与x之间的函数关系式.

查看答案和解析>>
科目:初中数学 来源: 题型:
 ,
,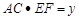 ,试求y与x之间的函数关系式.
,试求y与x之间的函数关系式.
查看答案和解析>>
科目:初中数学 来源:2012年濮阳第一中学中考模拟数学卷 题型:解答题
将□ABCD纸片沿EF折叠,使点C与点A重合,点D落在点G处.
1.求证:△ABE≌△AGF.
2.连结AC,若□ABCD的面积等于8,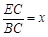 ,
, ,试求y与x之间的函数关系式.
,试求y与x之间的函数关系式.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com