
如图,△ABC内接与⊙O,AB是直径,⊙O的切线PC交BA的延长线于点P,OF∥BC交AC于AC点E,交PC于点F,连接AF.
(1)判断AF与⊙O的位置关系并说明理由;
(2)若⊙O的半径为4,AF=3,求AE的长.(2013舟山卷改编)
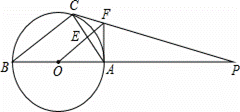
(1)AF为圆O的切线,理由为:
 连接OC,
连接OC,
 ∵PC为圆O切线,
∵PC为圆O切线,
 ∴CP⊥OC,
∴CP⊥OC,
 ∴∠OCP=90°,
∴∠OCP=90°,
 ∵OF∥BC,
∵OF∥BC,
 ∴∠AOF=∠B,∠COF=∠OCB, 2分
∴∠AOF=∠B,∠COF=∠OCB, 2分
 ∵OC=OB,
∵OC=OB,
 ∴∠OCB=∠B,
∴∠OCB=∠B,
 ∴∠AOF=∠COF,
∴∠AOF=∠COF,
 由△AOF≌△COF得,
由△AOF≌△COF得,
 ∴∠OAF=∠OCF=90°,
∴∠OAF=∠OCF=90°,
 则AF为圆O的切线; 4分
则AF为圆O的切线; 4分

 (2)∵△AOF≌△COF,
(2)∵△AOF≌△COF,
 ∴∠AOF=∠COF,
∴∠AOF=∠COF,
 ∵OA=OC,
∵OA=OC,
 ∴E为AC中点,即AE=CE=
∴E为AC中点,即AE=CE= AC,OE⊥AC,
AC,OE⊥AC,
 ∵OA⊥AF, 6分
∵OA⊥AF, 6分
 ∴在Rt△AOF中,OA=4,AF=3,
∴在Rt△AOF中,OA=4,AF=3,
 根据勾股定理得:OF=5,
根据勾股定理得:OF=5,
 ∵S△AOF=
∵S△AOF= •OA•AF=
•OA•AF= •OF•AE,
•OF•AE,
 ∴AE=
∴AE= , 8分
, 8分


 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:初中数学 来源: 题型:
如图,△ABC是格点三角形(三角形的三个顶点都是小正方形顶点)。
(1)将△ABC绕点C逆时针旋转90°,得到△CDE.写出点B对应点D和点A对应点E的坐标。
(2) 若以格点P、A、B为顶点的三角形与△CDE相似但不全等,请写出符合条件格点P的坐标。
 |
查看答案和解析>>
科目:初中数学 来源: 题型:
给出以下命题:
①已知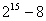 可以被在60~70之间的两个整数整除,则这两个数是63、65;
可以被在60~70之间的两个整数整除,则这两个数是63、65;
②若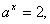
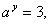 则
则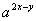 =
=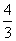 ;
;
③已知关于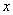 的方程
的方程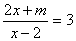 的解是正数,则m的取值范围为
的解是正数,则m的取值范围为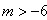 ;
;
其中正确的是( )
A.①② B.①② C.①③ D.②③
查看答案和解析>>
科目:初中数学 来源: 题型:
关于x的方程a(x+m)2+b=0的解是x1=-3,x2=5(a,m,b均为常数,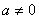 ),则方程a(x+m+2)2+b=0的解是____________.
),则方程a(x+m+2)2+b=0的解是____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
某工厂现在平均每天比原计算多生产50台机器,现在生产600台机器所需时间与原计划生产450台机器所需时间相同.设原计划平均每天生产x台机器,根据题意,下面所列方程正确的是
A.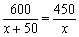 B.
B.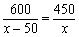
C.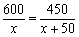 D.
D.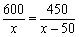
查看答案和解析>>
科目:初中数学 来源: 题型:
山东省第二十三届运动会将于2014年在济宁举行.下图是某大学未制作完整的三个年级省运会志愿者的统计图,请你根据图中所给信息解答下列问题:
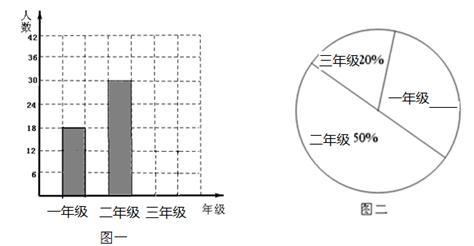
(1)请你求出三年级有多少名省运会志愿者,并将两幅统计图补充完整;
(2)要求从一年级、三年级志愿者中各推荐一名队长候选人,二年级志愿者中推荐两名队长候选人,四名候选人中选出两人任队长,用列表法或树形图,求出两名队长都是二年级志愿者的概率是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com