
【题目】对于给定的![]() ,我们给出如下定义:若点M是边
,我们给出如下定义:若点M是边![]() 上的一个定点,且以M为圆心的半圆上的所有点都在
上的一个定点,且以M为圆心的半圆上的所有点都在![]() 的内部或边上,则称这样的半圆为
的内部或边上,则称这样的半圆为![]() 边上的点M关于
边上的点M关于![]() 的内半圆,并将半径最大的内半圆称为点M关于
的内半圆,并将半径最大的内半圆称为点M关于![]() 的最大内半圆.若点M是边
的最大内半圆.若点M是边![]() 上的一个动点(M不与B,C重合),则在所有的点M关于
上的一个动点(M不与B,C重合),则在所有的点M关于![]() 的最大内半圆中,将半径最大的内半圆称为
的最大内半圆中,将半径最大的内半圆称为![]() 关于
关于![]() 的内半圆.
的内半圆.
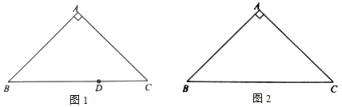
(1)在![]() 中,
中,![]() ,
,![]() ,
,
①如图1,点D在边![]() 上,且
上,且![]() ,直接写出点D关于
,直接写出点D关于![]() 的最大内半圆的半径长;
的最大内半圆的半径长;
②如图2,画出![]() 关于
关于![]() 的内半圆,并直接写出它的半径长;
的内半圆,并直接写出它的半径长;
(2)在平面直角坐标系![]() 中,点E的坐标为
中,点E的坐标为![]() ,点P在直线
,点P在直线![]() 上运动(P不与O重合),将
上运动(P不与O重合),将![]() 关于
关于![]() 的内半圆半径记为R,当
的内半圆半径记为R,当![]() 时,求点P的横坐标t的取值范围.
时,求点P的横坐标t的取值范围.
【答案】(1)①![]() ,②1,作图见详解;(2)t≥
,②1,作图见详解;(2)t≥![]() 或
或![]() .
.
【解析】
(1)①过点D作DE⊥AC,则以点D为圆心,DE长为半径的半圆与AC相切,利用等腰直角三角形的性质,即可求解;
②当点D为BC的中点时,以D为圆心,DE为半径的半圆就是![]() 关于
关于![]() 的内半圆,进而可求解;
的内半圆,进而可求解;
(2)设点P坐标为(t,![]() ),分两种情况分类讨论,①点P在第一象限时,②点P在第三象限时,分别求出t的取值范围,即可.
),分两种情况分类讨论,①点P在第一象限时,②点P在第三象限时,分别求出t的取值范围,即可.
(1)①如图1,过点D作DE⊥AC,则以点D为圆心,DE长为半径的半圆与AC相切,
∴D关于![]() 的最大内半圆的半径长就是DE的长,
的最大内半圆的半径长就是DE的长,
∵在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
∴DE=CD÷![]() =1÷
=1÷![]() =
=![]()
②如图2,当点D为BC的中点时,以D为圆心,DE为半径的半圆就是![]() 关于
关于![]() 的内半圆,
的内半圆,
∵在![]() 中,
中,![]() ,
,![]() ,DE⊥AC ,
,DE⊥AC ,
∴DE∥BA,
∴DE=![]() =
=![]() ×2=1;
×2=1;
(2)∵点P在直线![]() 上,
上,
∴∠POE=30°
设点P坐标为(t,![]() ),
),
∵点E的坐标为![]() ,
,
∴OE=3,
①若点P在第一象限时,设点M是线段OE上的动点,作MN⊥OP,MG⊥PE,
∵![]() ,
,
∴当R=![]() 时,如图3,则MN=MG=
时,如图3,则MN=MG=![]() ,OM=2×MN==2×
,OM=2×MN==2×![]() =
=![]() ,
,
∴ME=3-![]() =
=![]() ,
,
∴OM=ME,
在RtOMN和RtEMG中,
∵![]()
∴RtOMN RtEMG(HL)
∴∠MON=∠MEG=30°,
∴点P的横坐标t=![]() ,
,
当R=1时,如图4,则MN=1,OM=2×MN==2×1=2,此时,点P的横坐标t≥3,
∴t≥![]() 时,
时,![]() ;
;
②若点P在第三象限时,作 MG⊥PE,PH⊥x轴,
当R=![]() 时,如图5,则MG=MO=
时,如图5,则MG=MO=![]() ,
,
∴ME=3-MO=3-![]() =
=![]() ,
,
∴EG=![]() ,
,
∴tanE=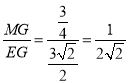 ,
,
∴![]() ,
,
∴ ,解得:
,解得:![]() ,
,
∴![]() 时,
时,![]() .
.
综上所述:t≥![]() 或
或![]() .
.
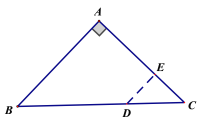
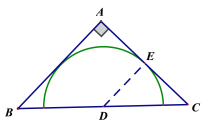
图1 图2
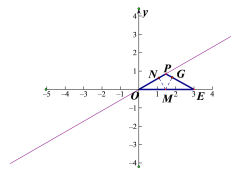
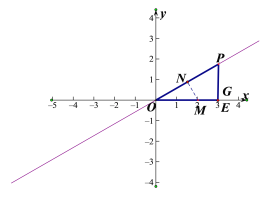
图3 图4
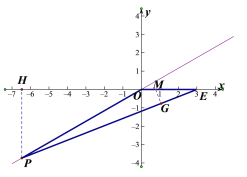
图5


科目:初中数学 来源: 题型:
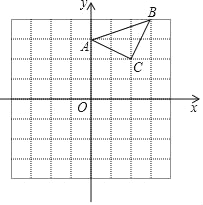
【题目】已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(0,3)、B(3,4)、C(2,2)(正方形网格中每个小正方形的边长是一个单位长度).
(1)画出△ABC向下平移4个单位长度得到的△A1B1C1,点C1的坐标是 ;
(2)以点B为位似中心,在网格内画出△A2B2C2,使△A2B2C2与△ABC位似,且位似比为2:1;
(3)四边形AA2C2C的面积是 平方单位.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 为倡导“低碳生活”,常选择以自行车作为代步工具,如图1所示是一辆自行车的实物图.车架档AC与CD的长分别为45cm,60cm,且它们互相垂直,座杆CE的长为20cm,点A,C,E在同一条直线上,且∠CAB=75°,如图2.
(1)求车架档AD的长;
(2)求车座点E到车架档AB的距离.
(结果精确到1 cm.参考数据: sin75°="0.966," cos75°=0.259,tan75°=3.732)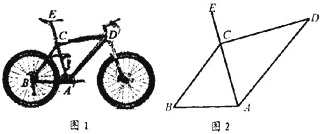
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售一批名牌衬衫,平均每天能售出20件,每件盈利40元。经调查发现:如果这种衬衫的售价每降低1元时,平均每天能多售出2件.设每件衬衫降价x元.
(1)降价后,每件衬衫的利润为_____元,销量为_____件;(用含x的式子表示)
(2)为了扩大销售,尽快减少库存,商场决定釆取降价措施。但需要平均每天盈利1200元,求每件衬衫应降价多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1是一个倾斜角为![]() 的斜坡的横截面,
的斜坡的横截面,![]() .斜坡顶端B与地面的距离
.斜坡顶端B与地面的距离![]() 为3米.为了对这个斜坡上的绿地进行喷灌,在斜坡底端安装了一个喷头A,喷头A喷出的水珠在空中走过的曲线可以看作抛物线的一部分.设喷出水珠的竖直高度为y(单位:米)(水珠的竖直高度是指水珠与地面的距离),水珠与喷头A的水平距离为x(单位:米),y与x之间近似满足函数关系
为3米.为了对这个斜坡上的绿地进行喷灌,在斜坡底端安装了一个喷头A,喷头A喷出的水珠在空中走过的曲线可以看作抛物线的一部分.设喷出水珠的竖直高度为y(单位:米)(水珠的竖直高度是指水珠与地面的距离),水珠与喷头A的水平距离为x(单位:米),y与x之间近似满足函数关系![]() (a,b是常数,
(a,b是常数,![]() ),图2记录了x与y的相关数据.
),图2记录了x与y的相关数据.
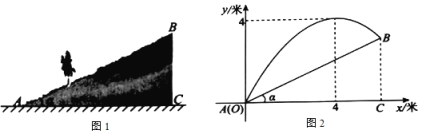
(1)求y关于x的函数关系式;
(2)斜坡上有一棵高1.8米的树,它与喷头A的水平距离为2米,通过计算判断从A喷出的水珠能否越过这棵树.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=mx2﹣(2m+1)x+m﹣5的图象与x轴有两个公共点.
(1)求m的取值范围;
(2)若m取满足条件的最小的整数,当n≤x≤1时,函数值y的取值范围是﹣6≤y≤24,求n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】校车安全是近几年社会关注的重大问题,安全隐患主要是超速和超载.某中学数学活动小组设计了如下检测公路上行驶的汽车速度的实验:先在公路旁边选取一点C,再在笔直的车道![]() 上确定点D,使CD与
上确定点D,使CD与![]() 垂直,测得CD的长等于21米,在
垂直,测得CD的长等于21米,在![]() 上点D的同侧取点A、B,使∠CAD=300,∠CBD=600.
上点D的同侧取点A、B,使∠CAD=300,∠CBD=600.
(1)求AB的长(精确到0.1米,参考数据:![]() );
);
(2)已知本路段对校车限速为40千米/小时,若测得某辆校车从A到B用时2秒,这辆校车是否超速?说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,抛物线![]() 与x轴交于A,B两点(点A在点B的左侧),交y轴于点C,经过B,C两点的直线为
与x轴交于A,B两点(点A在点B的左侧),交y轴于点C,经过B,C两点的直线为![]() .
.
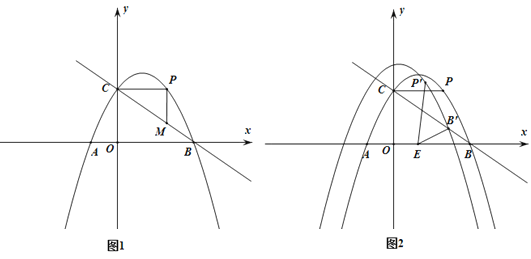
(1)求抛物线的函数表达式;
(2)点P为抛物线上的动点,过点P作x轴的垂线,交直线BC于点M,连接PC,若![]() 为直角三角形,求点P的坐标;
为直角三角形,求点P的坐标;
(3)当P满足(2)的条件,且点P在直线BC上方的抛物线上时,如图2,将抛物线沿射线BC方向平移,平移后B,P两点的对应点分别为![]() ,
,![]() ,取AB的中点E,连接
,取AB的中点E,连接![]() ,
,![]() ,试探究
,试探究![]() 是否存在最小值?若存在,求出这个最小值;若不存在,请说明理由.
是否存在最小值?若存在,求出这个最小值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】全民学习、终身学习是学习型社会的核心内容,努力建设学习型家庭也是一个重要组成部分.为了解“学习型家庭”情况,对部分家庭五月份的平均每天看书学习时间进行了一次抽样调查,并根据收集的数据绘制了下面两幅不完整的统计图,请根据图中提供的信息,解答下列问题:
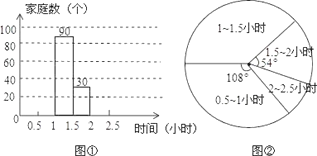
(1)本次抽样调查了 个家庭;
(2)将图①中的条形图补充完整;
(3)学习时间在2~2.5小时的部分对应的扇形圆心角的度数是 度;
(4)若该社区有家庭有3000个,请你估计该社区学习时间不少于1小时的约有多少个家庭?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com