练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，已知，为的直径，过点作弦垂直于直径于，点恰好为的中点，连接，．

    （1）求证：；

    （2）若，求的半径；

    （3）在（2）的条件下，求阴影部分的面积．

    【答案】（1）证明见解析；（2）的半径为2；（3）．

    【解析】

    （1）连接BD，根据圆周角定理得出∠CBD=∠AEB=90°，∠A=∠C，进而求得∠ABE=∠CDB，得出，即可证得结论；
    （2）根据垂径定理和圆周角定理易求得∠A=∠ABE，得出∠A=30°，解直角三角形求得AB，即可求得⊙O的半径；
    （3）根据S阴=S扇形-S△EOB求得即可．

    （1）证明：连接，

    ∵，为的直径，

    ∴，

    ∵点恰好为的中点，

    ∴，

    ∴，

    ∵，，

    ∴，

    ∴，

    ∴；

    （2）解：∵过点作弦垂直于直径于，

    ∴，

    ∵，

    ∴，

    ∴，

    ∴，

    在中，，

    ∴，

    ∴的半径为2．

    （3）连接，

    ∵，

    ∴，

    ∴是等边三角形，

    ∵，

    ∴，

    ∴．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】某社区为了加强社区居民对新型冠状病毒肺炎防护知识的了解，通过微信群宣传新型冠状病毒肺炎的防护知识，并鼓励社区居民在线参与《新型冠状病毒防治与预防知识》作答（满分100分），社区管理员随机从甲、乙两个小区各抽取20名人员的答卷成绩，并对他们的成绩（单位：分）进行数据统计、数据分析．

    甲

    85

    80

    95

    85

    90

    95

    100

    65

    75

    85

    90

    90

    70

    100

    90

    80

    80

    90

    98

    75

    乙

    80

    60

    80

    85

    95

    65

    90

    85

    100

    80

    95

    75

    80

    80

    70

    100

    95

    75

    90

    90

    表1分数统计表

    成绩

    小区

    60≤x≤70

    70＜x≤80

    80＜x≤90

    90＜x≤100

    甲

    2

    5

    a

    b

    乙

    3

    7

    5

    5

    表2：频数分布表

    统计量

    小区

    平均数

    中位数

    众数

    甲

    85.75

    87.5

    c

    乙

    83.5

    d

    80

    表3：统计量

    （1）填空：a=　 　，b=　 　，c=　 　，d=　 　；

    （2）甲小区共有800人参与答卷，请估计甲小区成绩大于90分的人数；

    （3）对于此次抽样调查中测试成绩为60≤x≤70的居民，社区鼓励他们重新学习，然后从中随机抽取两名居民进行测试，求刚好抽到一个是甲小区居民，另一个是乙小区居民的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某校为了解学生的安全意识情况，在全校范围内随机抽取部分学生进行问卷调查，根据调查结果，把学生的安全意识分成“淡薄”、“一般”、“较强”、“很强”四个层次，并绘制成如下两幅尚不完整的统计图．

    根据以上信息，解答下列问题：

    （1）这次调查一共抽取了 名学生，其中安全意识为“很强”的学生占被调查学生总数的百分比是 ；

    （2）请将条形统计图补充完整；

    （3）该校有1800名学生，现要对安全意识为“淡薄”、“一般”的学生强化安全教育，根据调查结果，估计全校需要强化安全教育的学生约有 名．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在3×3正方形方格中，有3个小正方形涂成了黑色，所形成的图案如图所示，图中每块小正方形除颜色外完全相同．

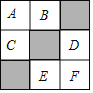
    （1）一个小球在这个正方形方格上自由滚动，那么小球停在黑色小正方形的概率是多少？

    （2）现将方格内空白的小正方形（A、B、C、D、E、F）中任取2个涂黑，得到新图案，请用列表或画树状图的方法求新图案是中心对称图形的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图是抛物线y＝ax2+bx+c（a≠0）的部分图象，其顶点坐标为（1，n），且与x轴的一个交点在点（3，0）和（4，0）之间，则下列结论：①4a﹣2b+c＞0；②3a+b＞0；③b2＝4a（c﹣n）；④一元二次方程ax2+bx+c＝n﹣1有两个互异实根．其中正确结论的个数是（　　）

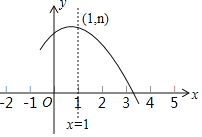
    A.1个B.2个C.3个D.4个

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在等腰△ABC中，AD⊥BC交直线BC于点D，若AD=BC，则△ABC的顶角的度数为_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，一次函数的图象与反比例函数在第一象限的图象交于和两点，与轴交于点连接

    （1）求反比例函数的解析式；

    （2）若点在轴上，且，求点的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为了满足学生的兴趣爱好，学校决定在七年级开设兴趣班，兴趣班设有四类：围棋班；象棋班；书法班；摄影班．为了便于分班，年级组随机抽查了部分学生的选课意向（每人选报一类），并绘制了如图所示的两幅统计图（不完整），请根据图中信息，解答下问题：

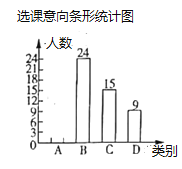
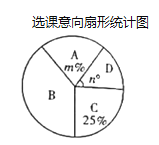
    （1）求扇形统计图中、的值，并补全条形统计图；

    （2）已知该校七年级有600名学生，学校计划开设三个“围棋班”，每班要求不超过40人，实行随机分班．

    ①学校的开班计划是否能满足选择“围棋班”的学生意愿，说明理由；

    ②展鹏、展飞是一对双胞胎，他们都选择了“围棋班”，并且希望能分到同一个班，用树状图或列表法求他们的希望得以实现的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，直线与轴交于点，与轴交于点，经过、两点的抛物线与轴的另一交点．

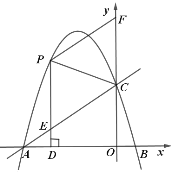
    （1）求该抛物线的函数表达式；

    （2）是该抛物线上的动点，过点作轴于点，交于点，交轴于点，设点的横坐标为．

    ①求出四边形的周长与的函数表达式，并求的最大值；

    ②当为何值时，四边形是菱形；

    ③是否存在点，使得以、、为顶点的三角形与相似？若存在，请求出满足条件的点的坐标；若不存在，请说明理由．

    查看答案和解析>>

    同步练习册答案