
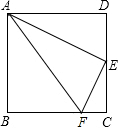
 如图,在正方形ABCD中,E是CD的中点,点F在BC上,且FC=$\frac{1}{4}$BC.则△ADE与△ECF是否相似?并说明理由.
如图,在正方形ABCD中,E是CD的中点,点F在BC上,且FC=$\frac{1}{4}$BC.则△ADE与△ECF是否相似?并说明理由. 分析 由正方形的性质得出BC=CD=AD,∠D=∠C=90°,再由已知条件得出AD=CD=2DE=2CE=4CF,证出$\frac{AD}{CE}=\frac{DE}{CF}$,即可得出△ADE∽△ECF.
解答 解:△ADE∽△ECF;理由如下:
∵四边形ABCD是正方形,
∴BC=CD=AD,∠D=∠C=90°,
∵E是CD的中点,FC=$\frac{1}{4}$BC,
∴AD=CD=2DE=2CE=4CF,
∵$\frac{AD}{CE}=2$,$\frac{DE}{CF}$=2,
∴$\frac{AD}{CE}=\frac{DE}{CF}$,
∴△ADE∽△ECF.
点评 本题考查了相似三角形的判定定理、正方形的性质;判定两三角形相似,除了要掌握定义外,还要注意正确找出两三角形的对应边、对应角,本题中的关键是证出两直角边对应成比例.


 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:初中数学 来源: 题型:选择题
| A. | y=x2-(x-2)2 | B. | x2+y-2=0 | C. | y=ax2+bx+c | D. | y=x2+3x-$\frac{1}{x}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 不变 | B. | 扩大到原来的3倍 | C. | 扩大到原来的9倍 | D. | 扩大到原来的6倍 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com