
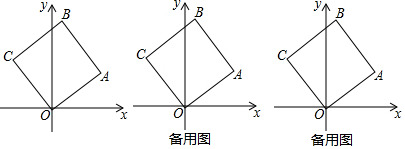
分析 (1)如图1中,作CM⊥x轴于,AN⊥x轴于N.连接AC、BO交于点K.易证△AON≌△COM,可得CM=ON=4,OM=AN=3,推出C(-3,4),由CK=AK,OK=BK,可得K($\frac{1}{2}$,$\frac{7}{2}$),B(1,7).
(2)分两种情形①当点Q在OA上时.②当点Q在OC上时.分别计算即可.
(3)分两种情形①当点A运动到点O时,t=3,当0<t≤3时,设O’C’交x轴于点E,作A’F⊥x轴于点F(如图3中).②当点C运动到x轴上时,t=4当3<t≤4时(如图4中),设A’B’交x轴于点F.分别求解即可.
解答 解:(1)如图1中,作CM⊥x轴于,AN⊥x轴于N.连接AC、BO交于点K.
易证△AON≌△COM,可得CM=ON=4,OM=AN=3,
∴C(-3,4),∵CK=AK,OK=BK,
∴K($\frac{1}{2}$,$\frac{7}{2}$),B(1,7),
故答案为-3,4,1,7.
(2)由题意得,AO=CO=BC=AB=5,
当t=2时,CP=2.
①当点Q在OA上时,∵PQ≥AB>PC,
∴只存在一点Q,使QC=QP.
作QD⊥PC于点D(如图2中),则CD=PD=1,
∴QA=2k=5-1=4,
∴k=2.
②当点Q在OC上时,由于∠C=90°所以只存在一点Q,使CP=CQ=2,
∴2k=10-2=8,∴k=4.
综上所述,k的值为2或4.
(3)①当点A运动到点O时,t=3.
当0<t≤3时,设O’C’交x轴于点E,作A’F⊥x轴于点F(如图3中).
则△A’OF∽△EOO’,
∴$\frac{EO′}{OO′}$=$\frac{A′F}{OF}$=$\frac{3}{4}$,OO′=$\frac{5}{3}$t,
∴EO′=$\frac{5}{4}$t,
∴S=$\frac{25}{24}$t2.
②当点C运动到x轴上时,t=4
当3<t≤4时(如图4中),设A’B’交x轴于点F,
则A’O=A′O=$\frac{5}{3}$t-5,
∴A′F=$\frac{5t-15}{4}$.
∴S=$\frac{1}{2}$($\frac{5t-15}{4}$+$\frac{5}{4}$t)×5=$\frac{50t-75}{8}$.
综上所述,S=$\left\{\begin{array}{l}{\frac{25}{24}{t}^{2}}&{(0<t≤3)}\\{\frac{50t-75}{8}}&{(3<t≤4)}\end{array}\right.$.
点评 本题考查四边形综合题、正方形的性质、坐标与图形的性质、等腰三角形的判定和性质、相似三角形的判定和性质等知识,解题的关键是学会用分类讨论的思想思考问题,属于中考压轴题.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
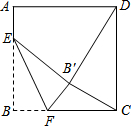 如图,正方形ABCD的边长是16,点E在边AB上,AE=3,动点F在边BC上,且不与点B、C重合,将△EBF沿EF折叠,得到△EB′F.
如图,正方形ABCD的边长是16,点E在边AB上,AE=3,动点F在边BC上,且不与点B、C重合,将△EBF沿EF折叠,得到△EB′F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com