
【题目】如图,在边长为 2 的正方形 ABCD 中剪去一个边长为 1 的小正方形 EFGD ,动点 P 从点 A 出发,沿A E F G C B 的路线,绕多边形的边匀速运动到点 B 时停止,则 ABP 的面积 S 随着时间t 变化的函数图象大致是( )

A. B.
B. C.
C. D.
D.
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线y=2x与反比例函数y= ![]() 在第一象限内的图象交于点A(m,2),将直线y=2x向下平移后与反比例函数y=
在第一象限内的图象交于点A(m,2),将直线y=2x向下平移后与反比例函数y= ![]() 在第一象限内的图象交于点P,且△POA的面积为2.
在第一象限内的图象交于点P,且△POA的面积为2.
(1)求k的值.
(2)求平移后的直线的函数解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某汽车销售公司4月份销售某厂汽车,在一定范围内,每辆汽车的进价与销售量有如下关系:若当月仅售出1辆汽车,则该汽车的进价为30万元,每多售出1辆,所有售出汽车的进价均降低0.1万元/辆,月底厂家一次性返利给销售公司,每辆返利0.5万元.
(1)若该公司当月售出5辆汽车,则每辆汽车的进价为 万元.
(2)若汽车的售价为31万/辆,该公司计划当月盈利12万元,那么需要售出多少辆汽车?(盈利=销售利润+返利)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线 AB与 x 轴,y 轴分别交于点 A和点 B,点 A的坐标为(1,0),且 2OA=OB.
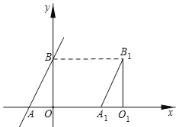
(1)求直线 AB 解析式;
(2)如图,将△A O B 向右平移 3 个单位长度,得到△A1O1B1,求线段 O B1的长;
(3)在(2)中△AOB 扫过的面积是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
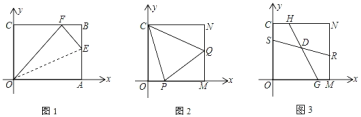
【题目】在平面直角坐标系xOy中,四边形OABC为矩形,OA在x轴正半轴上,OC在y轴正半轴上,且A(10,0)、C(0,8)
(1)如图1,在矩形OABC的边AB上取一点E,连接OE,将△AOE沿OE折叠,使点A恰好落在BC边上的F处,求AE的长;
(2)将矩形OABC的AB边沿x轴负方向平移至MN(其它边保持不变),M、N分别在边OA、CB上且满足CN=OM=OC=MN.如图2,P、Q分别为OM、MN上一点.若∠PCQ=45°,求证:PQ=OP+NQ;
(3)如图3,S、G、R、H分别为OC、OM、MN、NC上一点,SR、HG交于点D.若∠SDG=135°,HG=4![]() ,求RS的长.
,求RS的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
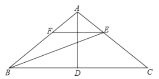
【题目】如图,在△ABC中,AB=AC,D是BC边上的中点,连接AD,BE平分∠ABC交AC于点E,过E作EF∥BC交AB于点F.
(1)若∠C=36°,求∠BAD的度数;
(2)求证:FB=FE.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com