
【题目】一架方梯长25米,如图,斜靠在一面墙上,梯子底端离墙7米.
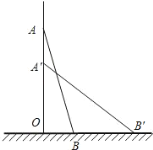
(1)这个梯子的顶端距地面有多高?
(2)如果梯子的顶端下滑了4米,那么梯子的底端在水平方向滑动了几米?
(3)当梯子的顶端下滑的距离与梯子的底端水平滑动的距离相等时,这时梯子的顶端距地面有多高?
【答案】(1)梯子距离地面的高度为24米;(2)梯子的底端在水平方向滑动了8米;(3)梯子顶端距离地面的高度为7米.
【解析】
(1)根据勾股定理即可求出答案;(2)由(1)可知梯子的顶端距地面有多高,从而可知梯子顶端下滑4米后距地面的距离,根据勾股定理即可求出梯子底部距离墙面的距离,从而得出答案;(3)设梯子的顶端下滑的距离与梯子的底端水平滑动的距离相等为x,根据勾股定理列式解答即可。
解:(1)根据勾股定理:梯子距离地面的高度为:![]() 米;
米;
(2)梯子下滑了4米,即梯子距离地面的高度为(24﹣4)=20米,
根据勾股定理:![]() ,解得A'B=8米.即下端滑行了8米.
,解得A'B=8米.即下端滑行了8米.
(3)设梯子的顶端下滑的距离与梯子的底端水平滑动的距离相等为x,
根据题意,![]() ,解得,x=17米,
,解得,x=17米,
即梯子顶端距离地面的高度为(24﹣17)=7米.
答:(1)梯子距离地面的高度为24米;(2)梯子的底端在水平方向滑动了8米;
(3)梯子顶端距离地面的高度为7米


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,AD是BC边上的高,CE平分∠ACB,AD与CE相交于点F.∠B=65°,∠AFC=120°,求∠BAD和∠ACB的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC,ΔDCE都是等边三角形,且B,C,E在同一条直线上,连接BD与AC交于点M,连接AE与CD交于点N,BD与AE交于点O.给出下列五个结论:①CD∥AB;②BD=AE;③CM=CN;④AO=OE;⑤∠AOD=120°.则其中正确结论有( )

A.5个B.4个C.3个D.2个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在等腰△OAB和等腰△OCD中,OA=OB,OC=OD,连接AC、BD交于点M.

(1)如图1,若∠AOB=∠COD=40°:
①AC与BD的数量关系为 ;
②∠AMB的度数为 ;
(2)如图2,若∠AOB=∠COD=90°:
①判断AC与BD之间存在怎样的数量关系?并说明理由;
②求∠AMB的度数;
(3)在(2)的条件下,当∠CAB=30°,且点C与点M重合时,请直接写出OD与OA之间存在的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 如图
如图![]() ,
,![]() 中,
中,![]() 平分
平分![]() 交
交![]() 于点
于点![]() ,在
,在![]() 上截取
上截取![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() .求证:四边形
.求证:四边形![]() 是菱形;
是菱形;
![]() 如图
如图![]() ,
,![]() 中,
中,![]() 平分
平分![]() 的外角
的外角![]() 交
交![]() 的延长线于点
的延长线于点![]() ,在
,在![]() 的延长线上截取
的延长线上截取![]() ,过点
,过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() .四边形
.四边形![]() 还是菱形吗?如果是,请证明;如果不是,请说明理由.
还是菱形吗?如果是,请证明;如果不是,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】寒假即将到来,某校为了解学生假期“最喜欢的健身项目”的情况,随机抽取了部分学生进行问卷调查,规定每人从“篮球”、“羽毛球”、“自行车”“爬山”和“其他”五个选项中必须选择且只能选择一个,并将调查结果绘制成如下两幅不完整的统计图表.
最喜爱的健身项目人数调查统计表
最喜爱的项目 | 人数 |
篮球 | 20 |
羽毛球 | 9 |
自行车 | 10 |
爬山 | a |
其他 | b |
合计 |
根据以上信息,请回答下列问题:

(1)这次调查的学生一共有多少人?并求a+b的值.
(2)扇形统计图中,“自行车”对应的扇形的圆心角为 度.
(3)结合自身的寒假健身计划,从以上五个选项中选择你所喜欢的一项健身项目是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AB=CD,BF=DE,AE⊥BD,CF⊥BD,垂足分别为E,F.

(1)求证:△ABE≌△CDF;
(2)若AC与BD交于点O,求证:AO=CO.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com