
 如图,两圆同心,半径分别为6与8,又矩形ABCD的边AB和CD分别为小大两圆的弦.则当矩形ABCD面积最大时,求此矩形的周长.
如图,两圆同心,半径分别为6与8,又矩形ABCD的边AB和CD分别为小大两圆的弦.则当矩形ABCD面积最大时,求此矩形的周长.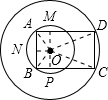 解:作OM⊥AD于点M,ON⊥AB于点N,OP⊥BC于点P.则四边形ANOM是矩形.
解:作OM⊥AD于点M,ON⊥AB于点N,OP⊥BC于点P.则四边形ANOM是矩形. S矩形AMPB,
S矩形AMPB, S矩形MPCD,
S矩形MPCD, S矩形ABCD.
S矩形ABCD. OA•OD•sin∠AOD=
OA•OD•sin∠AOD= ×6×8sin∠AOD=24sin∠AOD,
×6×8sin∠AOD=24sin∠AOD,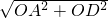 =
= =10,则BC=AD=10.
=10,则BC=AD=10. AD•OM=
AD•OM= OA•OB,
OA•OB,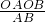 =
=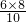 =4.8cm.
=4.8cm. S矩形AMPB,然后根据S△AOD=
S矩形AMPB,然后根据S△AOD= OA•OD•sin∠AOD,当∠AOD=90°,矩形的面积最大,即可求得AD的长,AB就是AD的弦心距的2倍,根据直角三角形的面积即可求解,进而求得矩形的周长.
OA•OD•sin∠AOD,当∠AOD=90°,矩形的面积最大,即可求得AD的长,AB就是AD的弦心距的2倍,根据直角三角形的面积即可求解,进而求得矩形的周长.

 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
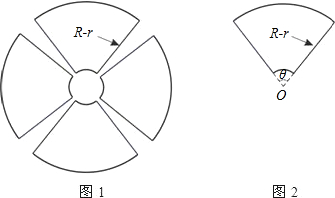 其中R、r分别为大圆和小圆的半径;
其中R、r分别为大圆和小圆的半径;查看答案和解析>>
科目:初中数学 来源: 题型:单选题
 如图所示,两圆同心,半径分别为9cm和5cm,另有一个圆与这两个圆都相切,则此圆的半径为
如图所示,两圆同心,半径分别为9cm和5cm,另有一个圆与这两个圆都相切,则此圆的半径为查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com