
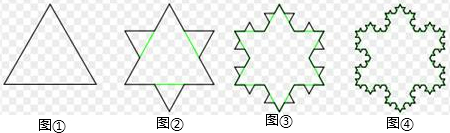
 如图,把一个正三角形分成四个全等的三角形,第一次挖去中间一个小三角形后剩下三个小正三角形,对剩下的三个小正三角形再重复以上做法,…,第n次挖去后剩下三角形的个数为( )
如图,把一个正三角形分成四个全等的三角形,第一次挖去中间一个小三角形后剩下三个小正三角形,对剩下的三个小正三角形再重复以上做法,…,第n次挖去后剩下三角形的个数为( )
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
| 256 |
| 27 |
| 256 |
| 27 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源:2013-2014学年浙江乐清育英寄宿学校九年级上学期期末考试数学试卷(解析版) 题型:解答题
把一个三角形分割成几个小正三角形,有两种简单的“基本分割法”.
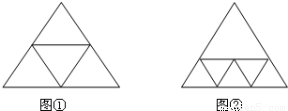
基本分割法1:如图①,把一个正三角形分割成4个小正三角形,即在原来1个正三角形的基础上增加了3个正三角形.
基本分割法2:如图②,把一个正三角形分割成6个小正三角形,即在原来1个正三角形的基础上增加了5个正三角形.
请你运用上述两种“基本分割法”,解决下列问题:
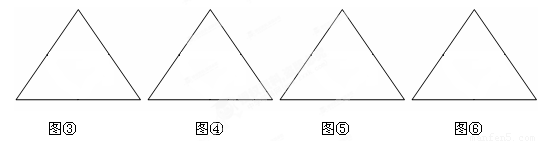
(1)把图③的正三角形分割成9个小正三角形;
(2)把图④的正三角形分割成10个小正三角形;
(3)把图⑤的正三角形分割成11个小正三角形;
(4)把图⑥的正三角形分割成12个小正三角形.
? 
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com