
【题目】如图,在每个边长都为![]() 的小正方形组成的网格中,小正方形的顶点叫做格点.线段
的小正方形组成的网格中,小正方形的顶点叫做格点.线段![]() 的端点
的端点![]() 均在格点上.
均在格点上.
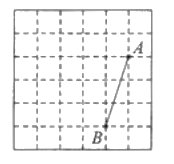
(1)线段![]() 的长度等于 ;
的长度等于 ;
(2)将线段![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到
得到![]() ,在图中画出
,在图中画出![]() ,并连结
,并连结![]() .
.
(3)在线段![]() 上确定一点
上确定一点![]() 连结
连结![]() ,使得
,使得![]() 与
与![]() 的面积比为
的面积比为![]() .
.
说明:以上作图只用无刻度的直尺画图,保留画图痕迹,不写画法.
科目:初中数学 来源: 题型:
【题目】如图所示,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于
的图象交于![]() .
.
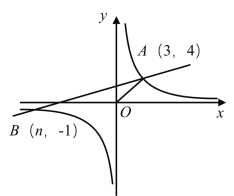
(1)求反比例函数和一次函数的解析式;
(2)在x轴上存在一点C,使![]() 为等腰三角形,求此时点C的坐标;
为等腰三角形,求此时点C的坐标;
(3)根据图象直接写出使一次函数的值大于反比例函数的值的x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市总预算![]() 亿元用三年时间建成一条轨道交通线.轨道交通线由线路敷设、搬迁安置、辅助配套三项工程组成.从2015年开始,市政府在每年年初分别对三项工程进行不同数额的投资.
亿元用三年时间建成一条轨道交通线.轨道交通线由线路敷设、搬迁安置、辅助配套三项工程组成.从2015年开始,市政府在每年年初分别对三项工程进行不同数额的投资.
2015年年初,对线路敷设、搬迁安置的投资分别是辅助配套投资的2倍、4倍.随后两年,线路敷设投资每年都增加![]() 亿元,预计线路敷设三年总投资为54亿元时会顺利如期完工;搬迁安置投资从2016年初开始遂年按同一百分数递减,依此规律,在 2017年年初只需投资5亿元,即可顺利如期完工;辅助配套工程在2016年年初的投资在前一年基础上的增长率是线路敷设2016年投资增长率的1.5倍,2017年年初的投资比该项工程前两年投资的总和还多4亿元,若这样,辅助配套工程也可以如期完工.经测算,这三年的线路敷设、辅助配套工程的总投资资金之比达到3: 2.
亿元,预计线路敷设三年总投资为54亿元时会顺利如期完工;搬迁安置投资从2016年初开始遂年按同一百分数递减,依此规律,在 2017年年初只需投资5亿元,即可顺利如期完工;辅助配套工程在2016年年初的投资在前一年基础上的增长率是线路敷设2016年投资增长率的1.5倍,2017年年初的投资比该项工程前两年投资的总和还多4亿元,若这样,辅助配套工程也可以如期完工.经测算,这三年的线路敷设、辅助配套工程的总投资资金之比达到3: 2.
(1)这三年用于辅助配套的投资将达到多少亿元?
(2)市政府2015年年初对三项工程的总投资是多少亿元?
(3)求搬迁安置投资逐年递减的百分数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某体育器材专卖柜经销A、B两种器材,A种器材每件进价350元,售价480元;B种器材每件进价200元,售价300元.
(1)该专卖柜计划用8000元去购进A、B两种器材若干件.
①若购进A种器材x件,B种器材y件,所获利润w元,请写出w与x之间满足的函数关系式;
②怎样购进才能使专卖柜经销这两种器材所获利润最大(其中A种器材不少于7件)?
(2)在“五·一”期间,该专卖柜对A、B两种器材进行如下优惠促销活动:
一次性购物总金额 | 优惠措施 |
不超过3000元 | 不优惠 |
超过3000元不超过4000元 | 售价打八折 |
超过4000元 | 售价打七折 |
促销活动期间:甲学校去该专卖柜购买A种器材付款2688元;乙学校去该专卖柜购买B种器材付款2100元,求丙学校决定一次性购买甲学校和乙学校购买的同样多的器材需付款多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市种植某种绿色蔬菜,全部用来出口.为了扩大出口规模,该市决定对这种蔬菜的种植实行政府补贴,规定每种植一亩这种蔬菜一次性补贴菜农若干元.经调查,种植亩数y(亩)与补贴数额x(元)之间大致满足如图所示的一次函数关系.随着补贴数额的不断增大,出口量也不断增加,但每亩蔬菜的收益z(元)会相应降低,且z与x之间也大致满足![]()
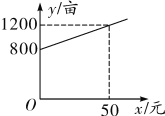
(1)求出政府补贴政策实施后,种植亩数y与政府补贴数额x之间的函数关系式;
(2)在政府出台补贴措施前,该市种植这种蔬菜的总收益额为多少?
(3)要使全市这种蔬菜的总收益w(元)最大,政府应将每亩补贴数额x定为多少?求出总收益w的最大值;
(4)该市希望这种蔬菜的总收益不低于7200000元,请你帮助该市确定每亩补贴数额的范围,在此条件下要使总收益最大,并说明每亩补贴数额应定为多少元合适?
参考公式:抛物线![]() 的顶点坐标是
的顶点坐标是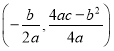 .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知:函数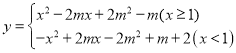 .
.
(1)当![]() 时,
时,
①求![]() 随
随![]() 增大而增大时,
增大而增大时,![]() 的取值范围;
的取值范围;
②当![]() 时,求
时,求![]() 的取值范围;
的取值范围;
③当![]() 时,设
时,设![]() 的最大值与最小值之差为
的最大值与最小值之差为![]() ,当
,当![]() 时,求
时,求![]() 的值.
的值.
(2)若![]() ,连结
,连结![]() .当此函数的图象与线段
.当此函数的图象与线段![]() 只有两个公共点时,直接写出
只有两个公共点时,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某厂将![]() 四种型号的空调销售额的情况绘制成了图①和图②两幅尚不完整的统计图.
四种型号的空调销售额的情况绘制成了图①和图②两幅尚不完整的统计图.
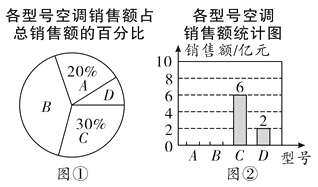
(1)请补全图②的条形统计图;
(2)为了应对激烈的市场竞争,该厂决定降价促销,![]() 四种型号的空调分别降价
四种型号的空调分别降价![]() ,因此该厂宣称其产品平均降价
,因此该厂宣称其产品平均降价![]() ,你认为该厂的说法正确吗?请通过计算说明理由;
,你认为该厂的说法正确吗?请通过计算说明理由;
(3)为进一步促销,该厂决定从这四种型号的空调中任意选取两种型号的空调降价销售,请用树状图或列表法求出降价空调中含D型号空调的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图①是甘肃省博物馆的镇馆之宝——铜奔马,又称“马踏飞燕”,于1969年10月出土于武威市的雷台汉墓,1983年10月被国家旅游局确定为中国旅游标志,在很多旅游城市的广场上都有“马踏飞燕”雕塑,某学习小组把测量本城市广场的“马踏飞燕”雕塑(图②)最高点离地面的高度作为一次课题活动,同学们制定了测量方案,并完成了实地测量,测得结果如下表:
课题 | 测量“马踏飞燕”雕塑最高点离地面的高度 | |||
测量示意图 |
| 如图,雕塑的最高点 | ||
测量数据 |
|
|
| 仪器 |
|
| 5米 |
| |
请你根据上表中的测量数据,帮助该小组求出“马踏飞燕”雕塑最高点离地面的高度(结果保留一位小数).(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() )
)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com