
【题目】如图,已知正方形ABCD的边长是5,点E在DC上,将△ADE经顺时针旋转后与△ABF重合.
(1)指出旋转的中心和旋转角度;
(2)如果连接EF,那么△AEF是怎样的三角形?请说明理由;
(3)△ABF向右平移后与△DCH位置,平移的距离是多少?
(4)试猜想线段AE和DH的数量关系和位置关系,并说明理由.
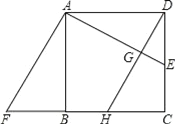
【答案】(1)旋转的中心是点A,旋转的角度是90°;(2)△AEF是等腰直角三角形(3)△ABF向右平移后与△DCH位置,平移的距离是5;(4)AE=DH,AE⊥DH,
【解析】(1)旋转的中心是点A,旋转的角度是90°;
(2)△AEF是等腰直角三角形.
理由如下:
∵△ADE绕点A顺时针旋转90°后与△ABF重合,
∴∠FAE=∠BAD=90°,AF=AE,
∴△AEF是等腰直角三角形.
(3)∵正方形ABCD的边长是5,
∴△ABF向右平移后与△DCH位置,平移的距离是5;
(4)AE=DH,AE⊥DH,
理由:∵△ABF向右平移后与△DCH重合,
∴DH∥AF,DH=AF,
又∵△ADE绕着点A顺时针旋转90°后与△ABF重合,
∴∠FAE=∠BAD=90°,AF=AE,
∴AE⊥AF,
∴AE=DH,AE⊥DH.
【试题分析】(1)根据旋转的定义,直接得出旋转的中心和旋转的角度;
(2)由(1)得到△ADE绕着点A逆时针旋转90°后与△ABF重合,根据旋转的性质得
∠FAE=90°,AF=AE,由此可判断△AEF是等腰直角三角形;
(3)利用旋转中心为正方形对角线的交点,逆时针旋转90°(或逆时针旋转270°),即可得出平移距离等于正方形边长;
(4)根据平移的性质得AF∥DH,由(2)得AF⊥AE,所以AE⊥DH,进而得出AE=DH.


 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:初中数学 来源: 题型:
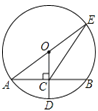
【题目】如图,⊙O的半径OD⊥弦AB于点C,连结AO并延长交⊙O于点E,连结EC.若AB=8,CD=2,则sin∠ECB为( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=kx-3与x轴、y轴分别相交于B、C两点,且OC=2OB
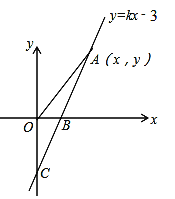
(1)求B点的坐标和k的值.
(2)若点A(x,y)是直线y=kx-3上在第一象限内的一个动点,当A 在运动的过程中,试写出△AOB的面积S与x的函数关系式,(不要求写出自变量的取值范围).
(3)探究:在(2)的条件下
①当A运动到什么位置时,△ABO的面积为![]() ,并说明理由.
,并说明理由.
②在①成立的情况下,x轴上是否存在一点P,使△AOP是等腰三角形?若存在,请直接写出满足条件的所有P点的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将一张矩形纸板按图中虚线裁剪成九块,其中有两块是边长都为![]() 的大正方形,两块是边长都为
的大正方形,两块是边长都为![]() 的小正方形,五块是长为
的小正方形,五块是长为![]() 、宽为
、宽为![]() 的全等小矩形,且
的全等小矩形,且![]() >
> ![]() .(以上长度单位:cm)
.(以上长度单位:cm)
(1)观察图形,可以发现代数式![]() 可以因式分解为 ;
可以因式分解为 ;
(2)若每块小矩形的面积为10![]() ,四个正方形的面积和为58
,四个正方形的面积和为58![]() ,试求图中所有裁剪线(虚线部分)长之和.
,试求图中所有裁剪线(虚线部分)长之和.

查看答案和解析>>
科目:初中数学 来源: 题型:
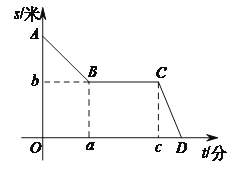
【题目】李老师为锻炼身体一直坚持步行上下班.已知学校到李老师家总路程为2000米.一天,李老师下班后,以45米/分的速度从学校往家走,走到离学校900米时,正好遇到一个朋友,停下又聊了半小时,之后以110米/分的速度走回了家.李老师回家过程中,离家的路程s(米)与所用时间t(分)之间的关系如图所示.
(1)求a,b,c的值;
(2)求李老师从学校到家的总时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察月历.
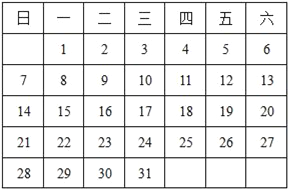
(1)根据月历中的规律填空:
| a |
|
|
(2)莉莉国庆假期外出旅行三天,三天日期之和是27,莉莉是 号出发的.
(3)某月小林连续三周周六外出参加羽毛球比赛并获得冠军,三天日期之和是51.
①小林是 号夺冠的.
②本月1号星期 .
查看答案和解析>>
科目:初中数学 来源: 题型:
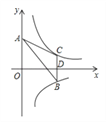
【题目】如图,两双曲线y=![]() 与y=﹣
与y=﹣![]() 分别位于第一、四象限,A是y轴上任意一点,B是y=﹣
分别位于第一、四象限,A是y轴上任意一点,B是y=﹣![]() 上的点,C是y=
上的点,C是y=![]() 上的点,线段BC⊥x轴于点 D,且4BD=3CD,则下列说法:①双曲线y=
上的点,线段BC⊥x轴于点 D,且4BD=3CD,则下列说法:①双曲线y=![]() 在每个象限内,y随x的增大而减小;②若点B的横坐标为3,则点C的坐标为(3,﹣
在每个象限内,y随x的增大而减小;②若点B的横坐标为3,则点C的坐标为(3,﹣![]() );③k=4;④△ABC的面积为定值7,正确的有( )
);③k=4;④△ABC的面积为定值7,正确的有( )
A. B. C. D. ④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com