

分析 (1)根据AP、PK是圆的半径可得出AP=PK,再由PA⊥y轴,PK⊥x轴,∠AOK=90°可得出结论;
(2))①连接PB,设点P(x,$\frac{2\sqrt{3}}{x}$),过点P作PG⊥BC于G,则半径PB=PC,由菱形的性质得PC=BC,可知△PBC为等边三角形,在Rt△PBG中,∠PBG=60°,PB=PA=x,PG=$\frac{2\sqrt{3}}{x}$,利用sin∠PBG=$\frac{PG}{PB}$,列方程求x即可;
②先根据菱形的性质得出P点坐标,再由待定系数法求出直线BP的解析式,设出M点的坐标,根据△MBP的面积等于菱形ABCP面积得出m的值,进而可得出点M的坐标.
解答 解:(1)四边形OKPA是正方形.
理由:∵AP、PK是圆的半径可,
∴AP=PK.
∵PA⊥y轴,PK⊥x轴,
∴∠PAO=∠PKO=90°.
∵∠AOK=90°,
∴四边形OKPA是正方形;
(2)①连接PB,设点P的横坐标为x,则其纵坐标为$\frac{2\sqrt{3}}{x}$.
过点P作PG⊥BC于G.
∵四边形ABCP为菱形,
∴BC=PA=PB=PC(半径).
∴△PBC为等边三角形.
在Rt△PBG中,∠PBG=60°,PB=PA=x,PG=$\frac{2\sqrt{3}}{x}$.
sin∠PBG=$\frac{PG}{PB}$,即$\frac{\sqrt{3}}{2}$=$\frac{\frac{2\sqrt{3}}{x}}{x}$.
解之得:x=±2(负值舍去).
∴PG=$\sqrt{3}$,PA=BC=2.
易知四边形OGPA是矩形,PA=OG=2,BG=CG=1,
∴OB=OG-BG=1,OC=OG+GC=3.
∴A(0,$\sqrt{3}$),B(1,0),C(3,0).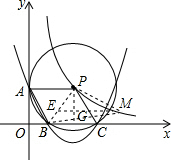
②∵A(0,$\sqrt{3}$),B(1,0),C(3,0),
∴P(2,$\sqrt{3}$).
设直线BP的解析式为y=kx+b(k≠0),则$\left\{\begin{array}{l}k+b=0\\ 2k+b=\sqrt{3}\end{array}\right.$,解得$\left\{\begin{array}{l}k=\sqrt{3}\\ b=-\sqrt{3}\end{array}\right.$,
∴直线BP的解析式为y=$\sqrt{3}$x-$\sqrt{3}$.
作ME∥x轴交PB于E,
设M(m,$\frac{2\sqrt{3}}{m}$),则E($\frac{2}{m}$+1,$\frac{2\sqrt{3}}{m}$),则ME=m-$\frac{2}{m}$-1,
∵△MBP的面积等于菱形ABCP面积,
∴$\frac{1}{2}$×$\sqrt{3}$(m-$\frac{2}{m}$-1)=2×$\sqrt{3}$,
化简得,m2-5m-2=0,解得m1=$\frac{5+\sqrt{33}}{2}$,m2=$\frac{5-\sqrt{33}}{2}$<0(舍去),
∴M($\frac{5+\sqrt{33}}{2}$,$\frac{3\sqrt{11}-5\sqrt{3}}{2}$).
点评 本题考查的是反比例函数综合题,涉及到反比例函数图象上点的坐标特点、利用待定系数法求一次函数的解析式、三角形的面积等知识,难度较大.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (2a-12)件 | B. | (2a+12)件 | C. | (2a-18)件 | D. | (2a+18)件 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com