
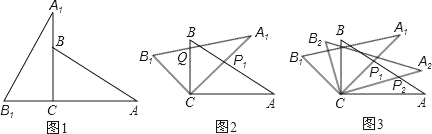
【题目】将两块全等的三角板如图1摆放,其中∠A1CB1=∠ACB=90°,∠A1=∠A=30°.
(1)将图1中△A1B1C绕点C顺时针旋转45°得图2,点P1是A1C与AB的交点,点Q是A1B1与BC的交点,求证:CP1=CQ;
(2)在图2中,若AP1=a,则CQ等于多少?
(3)将图2中△A1B1C绕点C顺时针旋转到△A2B2C(如图3),点P2是A2C与AP1的交点.当旋转角为多少度时,有△AP1C∽△CP1P2?这时线段CP1与P1P2之间存在一个怎样的数量关系?.
【答案】
【1】 ⑴证明:∵∠B1CB=45°,∠B1CA1=90°,∴∠B1CQ=∠BCP1=45°;
又B1C=BC,∠B1=∠B,∴△B1CQ≌△BCP1(ASA)∴CQ=CP1
【2】 ⑵解:作P1D⊥AC于D,∵∠A=30°∴P1D=![]() AP1;
AP1;
∵∠P1CD=45°,∴![]() =sin45°=
=sin45°=![]() ,∴CP1=
,∴CP1=![]() P1D=
P1D=![]() AP1;
AP1;
又AP1=![]() ,CQ=CP1 ,∴CQ=
,CQ=CP1 ,∴CQ=![]()
![]()
【3】 ⑶解:当∠P1CP2=∠P1AC=30°时,由于∠CP1P2=∠AP1C,
则△AP1C∽△CP1P2, 这时![]() ,
,
∴P1P2=![]() CP1 .
CP1 .
【解析】
试题(1)根据△A1B1C和△ABC是两个完全一样的三角形,顺时针旋转45°两个条件证明△B1CQ≌△BCP1,然后可求证:CP1=CQ;
(2)作P1D⊥AC于D,根据∠A=30,∠P1CD=45°分别求出P1D=![]() AP1,CP1=
AP1,CP1=![]() P1D=
P1D=![]() AP1,而AP1=a可求CQ.
AP1,而AP1=a可求CQ.
(3)当△A P1C∽△CP1P2时,∠P1CP2=∠P1AC=30°,再根据相似求出CP1与P1P2之间存在的数量关系;
试题解析:
(1)∵∠B1CB=45°,∠B1CA1=90°,
∴∠B1CQ=∠BCP1=45°;
又B1C=BC,∠B1=∠B,
∴△B1CQ≌△BCP1(ASA)
∴CQ=CP1;
(2)如图:作P1D⊥AC于D,
∵∠A=30°,
∴P1D=![]() AP1;
AP1;
∵∠P1CD=45°,
∴![]() =sin45°=
=sin45°=![]() ,
,
∴CP1=![]() P1D=
P1D=![]() AP1;
AP1;
又AP1=a,CQ=CP1,
∴CQ=![]() a;
a;
(3)当∠P1CP2=∠P1AC=30°时,由于∠CP1P2=∠AP1C,则△AP1C∽△CP1P2,
所以将图2中△A1B1C绕点C顺时针旋转30°到△A2B2C时,有△AP1C∽△CP1P2.
这时![]() =
=![]() =
=![]() ,
,
∴P1P2=![]() CP1.
CP1.


科目:初中数学 来源: 题型:
【题目】如图,二次函数![]() 的图象与
的图象与![]() 轴正半轴相交,其顶点坐标为
轴正半轴相交,其顶点坐标为![]() ,下列结论:①
,下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④方程
;④方程![]() 有两个相等的实数根,其中正确的结论是________.(只填序号即可).
有两个相等的实数根,其中正确的结论是________.(只填序号即可).
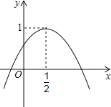
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校九年级学生开展踢毽子比赛活动,每班派5名学生参加,按团体总分多少排列名次,在规定时间内每人踢100个以上(含100个)为优秀.下表是成绩最好的甲班和乙班5名学生的比赛数据(单位:个):
1号 | 2号 | 3号 | 4号 | 5号 | 总成绩 | |
甲班 | 100 | 98 | 110 | 89 | 103 | 500 |
乙班 | 89 | 100 | 95 | 119 | 97 | 500 |
经统计发现两班总成绩相等,只好将数据中的其他信息作为参考.根据要求回答下列问题:
(1)计算两班的优秀率;
(2)求两班比赛数据的中位数;
(3)求两班比赛数据的方差;
(4)根据以上三条信息,你认为应该把冠军奖状发给哪一个班级?简述理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=60°,∠BAC的平分线AD与边BC的垂直平分线相交于点D,DE⊥AB交AB的延长线于点E,DF⊥AC于点F,现有下列结论:①DE=DF;②DE+DF=AD;③AM平分∠ADF;④AB+AC=2AE;其中正确的有( )

A.![]() 个B.
个B.![]() 个C.
个C.![]() 个D.
个D.![]() 个
个
查看答案和解析>>
科目:初中数学 来源: 题型:
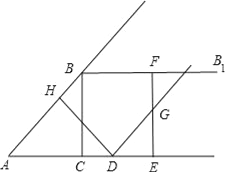
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,过点B作射线BB1∥AC.动点D从点A出发沿射线AC方向以每秒5个单位的速度运动,同时动点E从点C沿射线AC方向以每秒3个单位的速度运动.过点D作DH⊥AB于H,过点E作EF⊥AC交射线BB1于F,G是EF中点,连接DG.设点D运动的时间为t秒.
(1)当t为何值时,AD=AB,并求出此时DE的长度;
(2)当△DEG与△ACB相似时,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
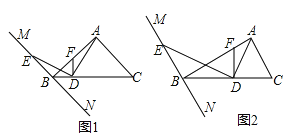
【题目】在Rt△ABC中,∠BAC=90°,过点B的直线MN∥AC,D为BC边上一点,连接AD,作DE⊥AD交MN于点E,连接AE.
(1)如图①,当∠ABC=45°时,求证:AD=DE;理由;
(2)如图②,当∠ABC=30°时,线段AD与DE有何数量关系?并请说明理由;
(3)当∠ABC=α时,请直接写出线段AD与DE的数量关系.(用含α的三角函数表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
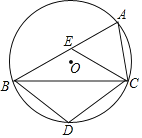
【题目】如图,△ABC是⊙O的内接三角形,点D在![]() 上,点E在弦AB上(E不与A重合),且四边形BDCE为菱形.
上,点E在弦AB上(E不与A重合),且四边形BDCE为菱形.
(1)求证:AC=CE;
(2)求证:BC2﹣AC2=ABAC;
(3)已知⊙O的半径为3.
①若![]() =
=![]() ,求BC的长;
,求BC的长;
②当![]() 为何值时,ABAC的值最大?
为何值时,ABAC的值最大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com