已知下面著名的“勾股定理”:在一个直角三角形中,两条直角边的平方之和等于斜边的平方.
试问:是否存在同时满足下列两个条件的直角三角形?
(1)三条边长均是正整数;
(2)一条直角边为素数(也称质数)p.若存在,请求出另一条直角边长;若不存在,请说明理由.
解:假设存在,令另一条直角边长为x,斜边长为y,则x、y为正整数.
由勾股定理得p
2+x
2=y
2.
化为(y+x)(y-x)=p
2.
因为p为素数(也称质数),且y+x>y-x,
所以只有

从而
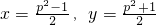
.
若p=2,则x、y不是整数,这样的三角形不存在;
若p为奇素数,x、y都是整数,这样的三角形存在.
综上所述,可知:p为偶素数2时,满足条件的三角形不存在;p为奇素数时,满足条件的三角形存在,且另一条直角边长为

.
分析:首先假设存在,设另一条直角边长为x,斜边长为y,则x、y为正整数,然后根据题意可得:p
2+x
2=y
2,即可得:(y+x)(y-x)=p
2,又由p为素数,讨论分析即可求得.
点评:此题考查了素数的意义和勾股定理等知识.难度较大,要注意分类讨论思想的应用.


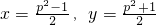 .
. .
.

 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案