
【题目】如图,点A在直线l上,点B在直线l外,点B关于直线l的对称点为C,连接AC,过点B作BD⊥AC于点D,延长BD至E使BE=AB,连接AE并延长与BC的延长线交于点F.

(1)补全图形;
(2)若∠BAC=2α,求出∠AEB的大小(用含α的式子表示);
(3)用等式表示线段EF与BC的数量关系,并证明.
【答案】(1)见解析;(2)∠AEB=![]() ;(3)BC=
;(3)BC=![]() ,证明见解析.
,证明见解析.
【解析】
(1)根据题意作图即可补全图形;
(2)先根据直角三角形两锐角互余的性质求出∠ABD,再由BE=AB,可得∠AEB=∠BAE,然后利用三角形的内角和定理即可求得结果;
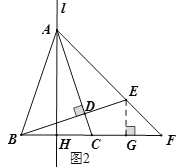
(3)设l与BC交于点H,过点E作EG⊥BF于点G,如图3,先利用轴对称的性推出∠BAH=∠CAH=α,再根据质余角的性质推出∠CBD=∠CAH=α,进一步利用(2)的结论和三角形的外角性质推出∠F=45°,进而可得![]() ,然后根据AAS可证明△ABH≌△BEG,从而得BH=EG,而BC=2BH,进一步即可得出EF与BC的数量关系.
,然后根据AAS可证明△ABH≌△BEG,从而得BH=EG,而BC=2BH,进一步即可得出EF与BC的数量关系.
解:(1)补全图形如图1所示:
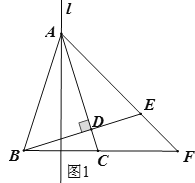
(2)∵BD⊥AC,∠BAD=2α,∴∠ABD=90°-2α,
∵BE=AB,∴∠AEB=∠BAE=![]() ;
;
(3)线段EF与BC的数量关系是:BC=![]() .
.
证明:设l与BC交于点H,过点E作EG⊥BF于点G,如图2,
∵点B关于直线l的对称点为C,∠BAC=2α,
∴BH=CH,∠BAH=∠CAH=α,
∵AH⊥BC,BD⊥AC,∴∠CAH+∠ACH=90°,∠CBD+∠ACH=90°,
∴∠CBD=∠CAH=α,
∵∠AEB![]() ,∠AEB=∠CBD+∠F,
,∠AEB=∠CBD+∠F,
∴∠F=45°,则△EFG为等腰直角三角形,∴![]() ,
,
∵∠BAH=∠EBG=α,∠AHB=∠BGE=90°,AB=BE,
∴△ABH≌△BEG(AAS),
∴BH=EG,
∵BC=2BH,∴BC=2EG=![]() .
.


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:初中数学 来源: 题型:
【题目】一块材料的形状是锐角三角形ABC,边BC=12cm,高AD=8cm,把它加工成矩形零件如图,要使矩形的一边在BC上,其余两个顶点分别在AB,AC上.且矩形的长与宽的比为3:2,求这个矩形零件的边长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在△ABC中,AB=AC,D是BC的中点,动点E在边AB上(点E不与点A,B重合), 动点F在射线AC上,连结DE, DF.
(1)如图1,当∠DEB=∠DFC=90°时,直接写出DE与DF的数量关系;

(2)如图2,当∠DEB+∠DFC=180°(∠DEB≠∠DFC)时,猜想DE与DF的数量关系,并证明;

(3)当点E,D,F在同一条直线上时,
①依题意补全图3;
②在点E运动的过程中,是否存在EB=FC? ( 填“存在”或“不存在” ).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AD平分∠BAC交BC于D,∠MDN的两边分别与AB,AC相交于M,N两点,且DM=DN.
(1)如图甲,若∠C=90°,∠BAC=60°,AC=9,∠MDN=120°,ND∥AB.
①写出∠MDA= °,AB的长是 .
②求四边形AMDN的周长;

(2)如图乙,过D作DF⊥AC于F,先补全图乙再证明AM+AN=2AF.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将线段![]() 绕点
绕点![]() 逆时针旋转角度
逆时针旋转角度![]() 得到线段
得到线段![]() ,连接
,连接![]() 得
得![]() ,又将线段
,又将线段![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得线段
得线段![]() (如图①).
(如图①).
![]() 求
求![]() 的大小(结果用含
的大小(结果用含![]() 的式子表示);
的式子表示);
![]() 又将线段
又将线段![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 得线段
得线段![]() ,连接
,连接![]() (如图②)求
(如图②)求![]() ;
;
![]() 连接
连接![]() 、
、![]() ,试探究当
,试探究当![]() 为何值时,
为何值时,![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,将一块含有![]() 角的三角板放置在一条直线上,
角的三角板放置在一条直线上,![]() 边与直线
边与直线![]() 重合,
重合,![]() 边的垂直平分线与边
边的垂直平分线与边![]() 分别交于
分别交于![]() 两点,连接
两点,连接![]() .
.


(1) ![]() 是 三角形;
是 三角形;
(2)直线![]() 上有一动点
上有一动点![]() (不与点
(不与点![]() 重合) ,连接
重合) ,连接![]() 并把
并把![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 到
到![]() ,连接
,连接![]() .当点
.当点![]() 在图2所示的位置时,证明
在图2所示的位置时,证明![]() .我们可以用
.我们可以用![]() 来证明
来证明![]() ,从而得到
,从而得到![]() .当点
.当点![]() 移动到图3所示的位置时,结论是否依然成立?若成立,请你写出证明过程;若不成立,请你说明理由.
移动到图3所示的位置时,结论是否依然成立?若成立,请你写出证明过程;若不成立,请你说明理由.
(3)当点![]() 在
在![]() 边上移动时(不与点
边上移动时(不与点![]() 重合),
重合),![]() 周长的最小值是 .
周长的最小值是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】李先生参加了清华同方电脑公司推出的分期付款购买电脑活动,他购买的电脑价格为![]() 万元,交了首付之后每月付款
万元,交了首付之后每月付款![]() 元,
元,![]() 月结清余款.
月结清余款.![]() 与
与![]() 的函数关系如图所示,试根据图象提供的信息回答下列问题.
的函数关系如图所示,试根据图象提供的信息回答下列问题.

![]() 确定
确定![]() 与
与![]() 的函数关系式,并求出首付款的数目;
的函数关系式,并求出首付款的数目;
![]() 如打算每月付款不超过
如打算每月付款不超过![]() 元,李先生至少几个月才能结清余款?
元,李先生至少几个月才能结清余款?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AC是⊙O的直径,弦BD⊥AO于E,连接BC,过点O作OF⊥BC于F,若BD=8cm,AE=2cm,则OF的长度是( )

A. 3cm B. ![]() cm C. 2.5cm D.
cm C. 2.5cm D. ![]() cm
cm
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com