

分析 因为等腰三角形腰的位置不明确,所以分(1)腰长在矩形相邻的两边上,(2)一腰在矩形的宽上,(3)一腰在矩形的长上,三种情况讨论.
解答 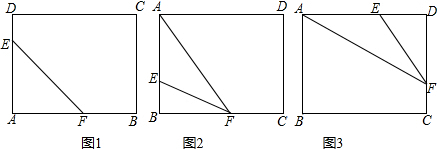 解:(1)当AE=AF=3时,如图1,
解:(1)当AE=AF=3时,如图1,
EF=$\sqrt{{3}^{2}+{3}^{2}}$=3$\sqrt{2}$;
(2)当AE=EF=3时,如图2,
则EB=4-3=1.FB=$\sqrt{E{F}^{2}-B{E}^{2}}$=$\sqrt{{3}^{2}-{1}^{2}}$=2$\sqrt{2}$,
则AF=$\sqrt{A{B}^{2}+B{F}^{2}}$=$\sqrt{{4}^{2}+(2\sqrt{2})^{2}}$=2$\sqrt{6}$;
(3)当AE=EF=3时,如图3,则ED=5-3=2.
DF=$\sqrt{E{F}^{2}-D{E}^{2}}$=$\sqrt{{3}^{2}-{2}^{2}}$=$\sqrt{5}$,
AF=$\sqrt{A{D}^{2}+D{F}^{2}}$=$\sqrt{30}$,
综上:等腰三角形的底边长为3$\sqrt{2}$cm,2$\sqrt{6}$cm,$\sqrt{30}$cm.
点评 本题考查了应用与设计作图,解决本题的关键是要根据三角形的腰长的不确定分情况讨论.


 优等生题库系列答案
优等生题库系列答案 53天天练系列答案
53天天练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知,如图,△ABC.
已知,如图,△ABC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 用圆规、直尺作图,不写作法.但要保留作图痕迹.
用圆规、直尺作图,不写作法.但要保留作图痕迹.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | AB=2,BC=4,AC=7 | B. | AB=5,BC=3,∠A=30° | ||
| C. | ∠A=60°,∠B=45°,AC=4 | D. | ∠C=90°,AB=6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com