
分析 根据根与系数的关系得到a+b=1,ab=-1,再利用完全平方公式变形得到$\frac{b}{a}$+$\frac{a}{b}$=$\frac{{b}^{2}+{a}^{2}}{ab}$=$\frac{(a+b)^{2}-2ab}{ab}$,然后利用整体代入的方法进行计算.
解答 解:∵实数a,b是方程x2-x-1=0的两根,
∴a+b=1,ab=-1,
∴$\frac{b}{a}$+$\frac{a}{b}$=$\frac{{b}^{2}+{a}^{2}}{ab}$=$\frac{(a+b)^{2}-2ab}{ab}$=-3.
点评 本题考查了根与系数的关系:若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-$\frac{b}{a}$,x1x2=$\frac{c}{a}$.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
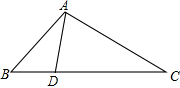 如图,点D在△ABC的边BC上,∠C+∠BAD=∠DAC,tan∠BAD=$\frac{4}{7}$,AD=$\sqrt{65}$,CD=13,则线段AC的长为4$\sqrt{13}$.
如图,点D在△ABC的边BC上,∠C+∠BAD=∠DAC,tan∠BAD=$\frac{4}{7}$,AD=$\sqrt{65}$,CD=13,则线段AC的长为4$\sqrt{13}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 880元 | B. | 800元 | C. | 720元 | D. | 1080元 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
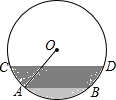 一条排水管的截面如图所示,已知排水管的半径OA=1m,水面宽AB=1.2m,某天下雨后,水管水面上升了0.2m,则此时排水管水面宽CD等于1.6m.
一条排水管的截面如图所示,已知排水管的半径OA=1m,水面宽AB=1.2m,某天下雨后,水管水面上升了0.2m,则此时排水管水面宽CD等于1.6m.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com