
���� ��1������ȥ���ţ��ɵô𰸣�
��2�����ݷ�ʽ�ļӼ����ɵô𰸣�
��� �⣺��1���ڢ۲����ִ���
����ȥ�����ŵ�����ʱ��������ĸ���û�б��
��2��ԭʽ=$\frac{x-3}{{x}^{2}-1}$-$\frac{2}{x-1}$
=$\frac{x-3}{��x+1����x-1��}$-$\frac{2��x+1��}{��x+1����x-1��}$
=$\frac{x-3-2x-2}{��x+1����x-1��}$
=$\frac{x-5}{��x+1����x-1��}$
=-$\frac{x+5}{{x}^{2}-1}$��
���� ���⿼���˷�ʽ�ļӼ�����ͨ�ֻ���ͬ��ĸ��ʽ���ټӼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ǧλ | B�� | ��λ | C�� | ��λ | D�� | ʮ��λ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
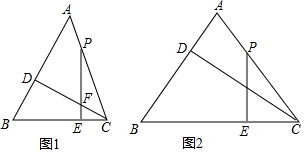
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
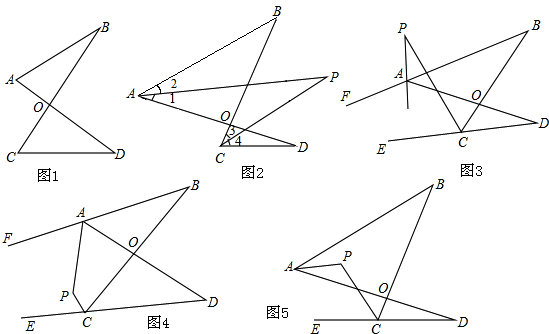
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
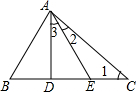 ��ͼ���ڡ�ABC�У������й�˵��������ǣ�������
��ͼ���ڡ�ABC�У������й�˵��������ǣ�������| A�� | ��ADB=��1+��2+��3 | B�� | ��ADE����B | C�� | ��AED=��1+��2 | D�� | ��AEC����B |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com